Data Types - Abstract Specification
 ANSI/HL7 V3 DT, R1-2004 11/29/2004 |
| Chair/Editor | Gunther Schadow gunther@aurora.rg.iupui.edu Regenstrief Institute for Health Care |
| Editor | Paul Biron paul.v.biron@kp.org Kaiser Permanente, Southern California |
| Editor | Lloyd McKenzie lmckenzi@ca.ibm.com IBM Global Services |
| Editor | Grahame Grieve grahame@kestral.com.au Kestral Computing Pty. Ltd. |
| Editor | Doug Pratt Douglas.Pratt@siemens.com Siemens |
Last Published: 09/26/2005 4:12 PM
HL7® Version 3 Standard, © 2005 Health Level Seven®, Inc. All Rights Reserved.
HL7 and Health Level Seven are registered trademarks of Health Level Seven, Inc. Reg. U.S. Pat & TM Off
Table of Contents
Appendices
Preface
1
Introduction
1.1
What is a Data Type?
Every data element has a data type. Data types define the meaning (semantics) of data values that can be assigned to a data element. Meaningful exchange of data requires that we know the definition of values so exchanged. This is true for complex "values" such as business messages as well as for simpler values such as character strings or integer numbers.
According to ISO 11404, a data type is "a set of distinct values, characterized by properties of those values and by operations on those values." A data type has intension and extension. Intentionally, the data type defines the properties exposed by every data value of that type. Extensionally, data types have a set of data values that are of that type (the type's "value set").
Semantic properties of data types are what ISO 11404 calls "properties of those values and [...] operations on those values." A semantic property of a data type is referred to by a name and has a value for each data value. The value of a data value's property must itself be a value defined by a data type - no data value exists that would not be defined by a data type.
Data types are thus the basic building blocks used to construct any higher order meaning: messages, computerized patient record documents, or business objects and their transactions. What, then, is the difference between a data type and a message, document, or business object? Data type values stand for themselves, the value is all that counts, neither identity nor state or changing of state is defined for a data value. Conversely in business objects, we track state and identity; the properties of an identical object might change between now and later. Not so with data values: a data value and its properties are constant. For example, number 5 is always number 5, there is no difference between this number 5 and that number 5 (no identity distinguished from value), number 5 never changes to number 6 (no change of state). One can think of data values as immutable objects where identity does not matter (identity and equality are the same.)1
1.2
Representation of Data Values
Data values can be represented through various symbols but the data value's meaning is not bound to any particular representation.
For example, cardinal numbers (non-negative integers) are defined - intentionally - as a data type where each value has a successor value, where zero is the successor of no other cardinal value. Based on this definition we can define addition, multiplication, and other mathematical operations. Whatever representation reflects the rules we stated in the intentional definition of the cardinal data type is a valid representation of cardinal numbers. Examples for valid cardinal number representations are decimal digit strings, bags of glass marbles, or scratches on a wall. The number five is represented by the word "five" by the Arabic number "5" or the Roman number "V". The representation does not matter as long as it conforms to the semantic definition of the data type.
Another example, the Boolean data type is defined by its extension, the two distinct values true and false and the rules of negation and combining these values in conjunction and disjunction. The representation of Boolean values can be the words "true" and "false," "yes" and "no," the numbers 0 and 1, any two signs that are distinct from each other. The representation of data types does not matter as long as it conforms to the semantic definition of the data type.
This specification defines the semantics, the meaning of the HL7 data types. This specification is about semantics only, independent from representational and operational concerns or specific implementation technologies. Additional standards for representing the data values defined here are being defined for various technological approaches. These standards are called "Implementable Technology Specification" (ITS.) Those ITS define how values are represented so that they conform to the semantic definitions of this specifications, this may include syntaxes for character or binary representations, and computer procedures to act on the representation of data values. The meaning of these ITS representations communicated, generated, and processed in computer programs, is defined based on this standard, the semantic data type specification.
1.3
Properties of Data Values
Data values have properties defined by their data type. The "fields" of "composite data types" are the most common example of such properties. However, more generally one should think of a data value's property as logical predicates or as mathematical functions; in simpler but still correct terms, properties are questions one can ask about a data value to receive another data value as an answer.
A property is referred to by its name. For example, the data type integer may have a property named "sign." A property has a domain, which is the set of possible "answer" values. The set of possible "answer" values is defined by the property's data type, but the domain of a property may be a subset of the data type's value set.
A property may also have arguments, additional information one must supply with a question to get an answer. For example, an important property of an integer number is that one integer plus another integer results in another integer, so the plus property of one integer needs an argument: the other integer.
Whether semantic properties have arguments is not a fundamentally relevant distinction. A data type's semantic property without arguments is not necessarily a "field" of a "composite" data type. For example, for integer values, we can define the property is-zero that has the Boolean value true when the number is zero and false when the number is not zero. This does not mean that is-zero must be an explicit component of any integer representation.
A data type's semantic property with arguments has no specific operational notions such as "procedure call," "passing arguments," "return values," "throwing exceptions," etc. These are all concepts of computer systems implementation of data types - but these operational notions are irrelevant for the semantics of data types.
This specification is about semantics of data types only. Neither is it about value representation syntax (not even an abstract syntax), nor is it about an operational interface to the data values.
1.4
Need for Abstraction
Why does this specification make such a big issue about its being abstract from representation syntax as well as operational implementation?
HL7 needs this kind of abstract semantic data type specification for a very practical purpose. One important design feature of HL7 version 3 is its openness towards representation and implementation technologies. All HL7 version 3 specifications are supposed to be done in a form independent from specific representation and implementation technologies. HL7 acknowledges that, while at times some representation and implementation technologies may be more popular than others, technology is going to change - and with changing technology, representations of data values will change. HL7 standards are primarily targeted to healthcare domain information, independent from the technology supporting this information. HL7 expects that specifications defined independent from today's technology will continue to be useful, even after the next technological "paradigm shift".
The issue of data types is closer to implementation technology than most other HL7 information standards - and therein lays a certain danger that we define data types too dependent on current implementation technologies.
The majority of HL7 standards are about complex business objects. Complex business objects with many informational attributes can be specified as abstract syntax, where components are eventually defined in terms of data types. Conversely, defining data types in terms of abstract syntax is of little use because the components of such abstract syntax constructs would still have to have data types.2
Why is this specification so circular? Why is the data type "ANY" defined in terms of specializations of itself?
This specification needs to be independent of any particular implementation, and is therefore abstract, and not intended to be implementable. In this sense, the circularity is not a problem, since it does not introduce any uncertainty about what this specification says.
Why doesn't this specification define a set of primitive data types based on which composite data types could be defined simply as abstract syntax?
Any concrete implementation of the HL7 standards must ultimately use the built-in data types of their implementation technology. Therefore, we need a very flexible mapping between HL7 abstract data types and those data types built into any specific implementation technology. With a semantic specification, an Implementable Technology Specification (ITS) can conform simply by stating a mapping between the constructs of its technology and the HL7 version 3 data type semantics. Whether a data type is primitive of composite is irrelevant from a semantic perspective, and the answer may be different for different implementation technologies.
For example, this standard specifies a character string as a data type with many properties (e.g., charset, language, etc.) However, in many Implementation Technologies, character strings are primitive first class data types. We encourage that these native data types be used rather than a structure that slavishly represents all the semantic properties as "components." This specification only requires that the properties defined for data values can somehow be inferred from whatever representation is chosen, it does not matter how these values are represented. Whether "primitive" or "composite", with few or many "components", as "fields" or "methods" - this is all irrelevant.
For another example, a decimal representation, a floating-point register and a scaled integer are all possible native representations of real numbers for different implementation technologies. Some of these representations have properties that others do not have. Scaled integers, for instance, have a fixed precision and a relatively small range. Floating-point values have variable precision and a large range, but floating-point values lose any information about precision. Decimal representations are of variable precision and maintain the precision information (yet are slow to processing.) The data type semantics must be independent from all these accidental properties of the various representations, and must define the essential properties that any technology should be able to represent.
1.5
Need for an HL7 Data Type Standard
Why does HL7 need its own data type standard? Why can't HL7 simply adopt a standard defined by some other body?
As noted in the previous section, all HL7 implementation technologies have some data type system, but there are differences among the data type systems between implementation technologies. In addition, many implementation technologies' data type systems are not powerful enough to express the concepts that matter for the HL7 application layer.
For example, few implementation technologies provide the concepts of physical quantities, precision, ranges, missing information, and uncertainty that are so relevant in scientific and health care computing.
On the other hand, implementation technologies do make distinctions that are not relevant from the abstract semantics viewpoint, e.g., fixed point vs. floating-point real numbers; 8, 16, 32, or 64-bit integers; date vs. timestamp.
A number of data type systems have been used as input to this specification. These include the type systems of many major programming languages, including BASIC, Pascal, MODULA-2, C, C++, JAVA, ADA, LISP and SCHEME. This also includes type systems of language-independent implementation technologies, such as Abstract Syntax Notation One (ASN.1), Object Management Group's (OMG) Interface Definition Language (IDL) and Object Constraint Language (OCL), SQL 92 and SQL 99, the ISO 11404 language independent data types, and XML Schema Part 2 data types. Health care standards related data types have been considered as well, among these HL7 version 2.x, types used by CEN TC 251 messages and Electronic Health Record Architecture (EHCRA) and DICOM.
1.6
Requirements
The data types described in this specification are designed to meet a number of requirements. These include
- Modelling considerations
- Implementation Considerations
- Compatibility with other data type standards
- Functional Requirements identified in other HL7 standards where the data types are used
Of these, the last is the most important consideration. These data types are designed to deliver the functionality required throughout the HL7 standards. These requirements are not always compatible, and throughout this specification there is a number of places where particular design features are less than optimal for one of the 4 considerations listed above. In a number of these places, the requirements that led to this design feature are described in a requirements section. These requirements sections are only informative, not normative.
| Requirement The Reference Information Model defines a number of reference classes on which all domain information models are based. Each of these reference classes has a series of attributes which has an assigned type. Where the reference classes are used (cloned into) in domain models, the types in the reference classes may be replaced by other types to clarify and constrain the use of the attribute in the clone classes. This data types specification must define the rules for which data types can be substituted in this fashion. This specification chooses to use the specialization metaphor as a basis for the substitution rules, since this is widely understood and used method in theory and practice, and because these rules are more easily understood and managed than the alternatives. This use of specialization may lead to designs that may appear unfamiliar to some. |
1.7
Forms of Data Type Definitions
This specification defines data types in several forms, using textual description, UML diagrams, tables, and a formal definition.
1.7.1
Formal Data Type Definition Language
A formal definition of data types is used in order to clarify the semantics of the proposed types as unambiguously as possible. This data type definition language is described in detail in Introduction to the Formal Data Type Definition Language (DTDL) (§ 1.9 ). Formal languages make crisp essential statement and are therefore accessible to some formal argument of proof or rebuttal. However, the terseness of such formal statements may also be difficult to understand by humans. Therefore, all the important inferences from the formal statements are also included as plain English statements.
1.7.2
Tables of Properties
For a quick overview at the beginning of many data types this specification contains tables listing "primary" properties. "Primary" properties are a somewhat fuzzy notion of those properties that are more likely to be thought of as "fields" when the data type where implemented as a record, or that are expected to be used more often. These tables are provided to facilitate an overview of the content and purpose of data types. There is no requirement that the properties listed in these tables be represented as fields, and these tables are not abstract syntax definitions.
Each row of the property tables describes one property with the following columns:
- Name - the name of the property as stated in the formal definition. For some data types, the name field of the first property may be empty. This may happen in those data types that are defined as extension of other data types and when it is not useful for the summary of the child to show any properties of the parent.
- Type - the data type of that property.
- Definition - a short text describing the meaning of the property.
1.7.3
Unified Modeling Language (UML) Diagrams
The Unified Modeling Language (UML) is used for a graphical presentation of how data types relate to each other . Data types are shown as UML classes using the shortname for the class. Properties of types are shown as UML operations. Generic types are shown as UML parameterized classes, with UML realization links relating their instantiations.
Much of the detail of the data type declarations cannot be represented in the UML representation. Therefore the formal definition of the data types in the Data Type Definition Language (DTDL) should be used for detailed specification of the data types.
Some of the constraints from the DTDL are represented as constraints on the operations. Where constrains are shown, they are statements that will be true and are taken from the DTDL specification
The UML Diagrams use a stereotype "mixin". The mixin stereotype applies to a parameterized class, and denotes that the class specializes the parameter type and expresses all the properties of the type T in addition to it's own properties
1.8
Overview of Data Types
1.9
Introduction to the Formal Data Type Definition Language (DTDL)
NOTE: This is not an API specification. While this formal language might resemble some programming language or interface definition language, it is not intended to define the details of programs and other means of implementation. The formal definitions are a normative part of this specification, but this particular language needs not be implemented or used in conformant systems; nor need all the semantic properties be implemented or used by conformant systems. The internal working of systems, their way to implement data types, their functionality and services is entirely out of scope of this specification. The formal definition only specifies the meaning of the data values through making statements how one would theoretically expect these values to relate and behave.
This formal data type definition language3 specifies:
- type name and short name;
- named values of a fully enumerated extension;
- semantic properties, unary, binary, and higher order properties;
- invariants, i.e. constraints over the properties.
- allowable type conversions;
- syntax of character string value literals (if any);
Definition of a data type occurs in two steps. First, the data type is declared. The declaration claims a name for a new data type with a list of names, types, and signatures of the new type's semantic properties. This declares, not defines the type. The definition occurs in both logic statements about what is always true about this type's values and their properties (invariant statements.)
1.9.1
Declaration
Every data type is declared in a form that begins with the keyword type. For example, the following is the header of a declaration for the data type Boolean that has the short name alias BL and specializes the data type ANY.4
|
The Boolean data type declaration also contains a values-clause that declares the Boolean's complete set of values (its extension) as named entities. These named values are also valid character string literals. None of the other data types defined in this specification has a finite value set, which is why the values-clause is unique to the Boolean. In the marked-up formal language, value names use Italics font.
The block in curly braces following the header contains declarations of the semantic properties that hold for every value of the data type. A semicolon terminates each property declaration; and another semicolon after the closing curly brace terminates the data type declaration.
A property declaration mentions from left to right: (1) the data type of the property's value domain, (2) the property name, and (3) an optional argument list. The argument list of a property is enclosed in parentheses containing a sequence of argument declarations. Each argument is declared by the data type name and argument name. Semantic properties without arguments do not use an empty argument list.5
The specializes-clause means (a) inheritance of properties from the genus to the species, and (b) substitutability of values of the species type for variables of the genus type. Specialization can include the definition of additional properties and the specification of constraints on inherited properties for the specialized type.
An example for inheritance is: when CD has the property code and CS specializes CD then CS also has this property code even though isNull is not listed explicitly in the property declaration of BL. An example for substitutability is: when a property is declared as of a data type CD, and CS specializes CD, then a value of such property may be of type CS. In other words, substitutability is the same as subsumption of all values of type CS being also values of type CD.6
The type-declaration may be qualified by the keyword abstract, protected., or private. An abstract type is a type where no value can be just of this type without belonging to a concrete specialization of the abstract. A protected type is a type that is used inside this specification but no property outside this specification should be declared of a protected type. A private type is an internal "helper" abstraction, defined only for the purpose of defining some aspect of the semantics of deata types but that is not used even as the type of another protected or public type's property.7 (We also use the qualifier private at one point. Private types are only specified for the sake of formal definition of other types and are not used in any form outside this specification.)
1.9.2
Invariant Statements
The declaration of semantic properties, their names, data types, and arguments provide only clues as to what the new data type might be about. The true definition lies in the invariant statements. Invariant statements are logical statements that are true at all times.
Throughout this specification, invariant statements are provided in a formal syntax but are also written in plain English. The advantage of the formal syntax is that it can be interpreted unambiguously, and that it is strongly typed. The advantage of plain English statements is that they are more understandable, especially to those untrained in reading formal languages.
The formal syntax does help to sharpen the decisiveness of this specification. In some cases, however, the full semantics of a type are beyond what can be fully expressed in such invariant statements. The combination of both plain and formal language helps to make this specification more clear.
Invariant statements are formed using the invariant keyword that declares one or more variables in the same form as an argument list of a property. The invariant statement can contain a where clause that constrains the arguments for the entire invariant body. The invariant body is enclosed in curly braces. It contains a list of assertions that must all be true.
|
The semantics of the invariant statement is a logic predicate with a universal quantifier ("for all").
The above invariant statement can be read in English as "For all Boolean values x, where x is non-NULL it holds that x AND true equals x." All properties should be named such that one can read the assertions like English sentences.8
The argument list of an invariant statement need not be specified if no such argument is needed.
|
1.9.2.1
Assertion Expressions
Assertions in invariant statements are expressions built with the semantic properties of defined data types. Assertion expressions must have a Boolean value (true or false.)9 No primitive data types, or operations, pre-exist the definition of any data type. The only preexisting features of the assertion expression language are:10
- character strings representing utterances in the data type definition language;
- the notion of an assertion being successful (true) or failing (false);
- the invariant statement: invariant(...) where ... {...};
- the universal quantifier expression form forall (...) where ... {...}; synonymous to the invariant statement;
- the existence quantifier expression form exists (...) where ... {...};
- the implicit conjunction (logical AND) between the semicolon-separated assertions: assertion1; assertion2; ... ; assertionn;
- variables and declarations in the invariant argument list;
- the property reference using the period: x.property;
- implicit and explicit type conversion: (T)x;
- parentheses to override the priorities of the conversion and property resolution operators: (T)x.property versus((T)x).property.
1.9.2.2
Nested Quantifier Expressions
Within assertion expressions, nested quantifier statements can be formed similar to invariant statements. In fact, the universal quantifier built using the forall keyword is the same as the invariant statement. The universal quantifier can be used in a nested expression when the complexity of the problem requires it, such as in the following example:
|
The existence quantifier has the meaning as in common propositional logic. For example, the following invariant means: "SET values x and y intersect if and only if there exists an element e that is contained in both sets x and y."
|
The existence quantifier may have a where-clause; however, there is no difference whether an assertion is made as a where-clause or in the body of the existence quantifier. Conversely, for universal quantifiers, the where-clause weakens the assertion since the body now only applies for values that meet the criterion in the where-clause.
1.9.3
Type Conversion
This specification defines certain allowable conversions between data types. For example, there is a pair of conversions between the Character String (ST) and Encode Data (ED). This means that if a one expects an ED value but actually has an ST value instead, one can turn the ST value into an ED.11
Three kinds of type conversions are defined: promotion, demotion, and character string literals. Type conversions can be implicit or explicit. Implicit type conversion occurs when a certain type is expected (e.g. as an argument to a statement) but a different type is actually provided. If the type provided has a conversion to the type expected the conversion should be done implicitly.
NOTE: An Implementation Technology Specification will have to specify how implicit type conversions are supported. Some technologies support it directly others do not; in any case, processing rules can be set that specify how these conversions are realized.
An explicit conversion can be specified in an assertion expression using the converted-to type name in parenthesis before the converted value. For example the following is an explicit type conversion in the where clause of an invariant statement.
|
The type conversion has lower priority than the property resolution period. Thus "(T)a.b " converts the value of the property b of variable a to data type T while "((T)a).b " converts the value of variable a to T and then references property b of that converted value.
Implicit type conversions in the assertion expressions are performed where possible. If a property's formal argument is declared of data type T; but the expression used as an actual argument is of type U; and if U does not extend T; and if U defines a conversion to T, that conversion from T to U takes effect.
1.9.3.1
Demotion
A demotion is a conversion with a net loss of information. Generally, this means that a more complex type is converted into a simple type.
An example for a demotion is the conversion from Interval (IVL) to a simple Quantity (QTY), e.g. the center of the interval. In the data type definition language, a demotion is declared using the keyword demotion and the data type name to which to demote:
|
The specification of demotions shall indicate what information is lost and what the major consequences of losing this information are.
1.9.3.2
Promotion
A promotion is a conversion where new information is generated. Generally, this means that a simpler type is converted into a more complex type.
For example, we allow any Quantity (QTY) to be converted to an Interval (IVL). However, IVL has more semantic properties than QTY, low and high boundary. Thus, the conversion of QTY to IVL is a promotion. The additional properties of QTY not present in IVL must assume new values, default values, or computed values. The specification of the promotion must indicate what these values are or how they can be generated.
A promoting conversion from type QTY to type IVL is defined as a semantic property of data type QTY using the keyword promotion and the data type name to which to promote:
|
Typically, a promotion is defined from a simple type to a more complex type. Also typically, the simple type is declared earlier in this document than a more complex type. Declaring all promotions to complex types in the simple type would thus involve forward references and would be confusing to the reader. Therefore, an alternative syntax allows promotions to be defined in the more complex type. This is indicated by naming the type from which to promote in an argument list behind the type to which to promote.
|
1.9.4
Literal Form
A literal is a character string representation of a data value. Literals are defined for many types. A literal is a type conversion from and to a Character String (ST) with a specially defined syntax.
Not every conversion from and to an ST is a literal conversion, however. A literal for a data type should be able to represent the entire value set of a data type whereas any other conversion to and from ST may only map a smaller subset of the converted data type.
The purpose of having literals is so that one can write down values in a short human readable form. For example, literals for the types integer number (INT) and real number (REAL) are strings of sign, digits, possibly a decimal point, etc. The more important interval types (IVL<REAL>, IVL<PQ>, IVL<TS>) have literal representations that allow one to use, e.g., "<5" to mean "less than 5", which is much more readable than a fully structured form of the interval. For some of the more advanced data types such as intervals, general timing specification, and parametric probability distribution we expect that the literal form may be the only form seen for representing these values until users have become used to the underlying conceptualizations.
Each literal conversion has its own syntax (grammar,) often aligned with what people find intuitive. This syntax may therefore not be completely straightforward from a computer's perspective.12
NOTE: Character string based Implementable Technology Specifications (ITS) of these abstract data types may or may not choose the literals defined here as their representations for these data types. We expect that the XML ITS, will use some but not all of the literals defined here.
1.9.4.1
Declaration
In the data type definition language we declare a literal form as a property of a data type using the keyword literal followed by the data type name ST, since the literal is a conversion to and from the ST data type.
|
1.9.4.2
Definition
The actual definition of the literal form occurs outside the data type declaration body using an attribute grammar. An attribute grammar is a grammar that specifies both syntax and semantics of language structures. The syntax is defined in essentially the Backus-Naur-Form (BNF).13
For example, consider the following simple definition of a data type for cardinal numbers (positive integers.) This type definition depends only the Boolean data type (BL) and has a character string literal declared:
|
The literal syntax and semantics is first exposed completely and then described in all detail.
|
Every syntactic rule consists of the name of a symbol, a colon and the definition (so called production) of the symbol. A production is a sequence of symbols. These other symbols are also defined in the grammar, or they are terminal symbols. Terminal symbols are character strings written in double quotes or string patterns (called regular expressions.) Thus the form:
|
means, that any cardinal number symbol is a cardinal number symbol followed by a digit or just a digit. The vertical bar stands for a disjunction (logical OR.) A syntactic rule ends with a semicolon.
Every symbol has exactly one value of a defined data type. The data type of the symbol's value is declared where the symbol is defined:
|
means that the symbol digits has a value of type CARD. The start-symbol is the data type itself and does not need a separate name.
The semantics of the literal expression is specified in semantic rules enclosed in curly braces for each of the defined productions of a symbol:
symbol : production1 { rule1 } | production2 { rule2 } | ... | productionn { rulen };
A semantic rule is simply a semicolon-separated list of Boolean assertion expressions of the same kind as those used in invariant statements. However, there are special variables defined in the semantic rule that all begin with a dollar character (e.g., $, $1, $2, $3, ...) The simple $ stands for the value of the currently defined symbol; while $1, $2, $3, etc. stand for the values of the parts of the semantic rule's associated production. For example, in
|
the first production "CARD digit" has a semantic rule that says: the value $ of the defined symbol equals the value $1 of the first symbol CARD times ten plus the value $2 of the second symbol digit.14
A terminal symbol can be specified as a string pattern, so-called regular expression. The regular expression syntax used here is the classic syntax invented by Aho and used in AWK, LEX, GREP, and PERL. Regular expressions appear between two slashes /.../. In a regular expression pattern every character except [ ] ^ $ . / : ( ) \ | ? * + { } matches itself. The other characters that are actually used in this specification are defined in Table 2.
1.9.5
Generic Data Types
Generic data types are incomplete type definitions. This incompleteness is signified by one or more parameters to the type definition. Usually parameters stand for other types. Using parameters, a generic type might declare semantic properties of other not fully specified data types. For example, the generic data type Interval is declared with a parameter T that can stand for any Quantity data type (QTY). The components low and high are declared as being of type T.
|
Instantiating a generic type means completing its definition. For example, to instantiate an Interval, one must specify of what base data type the interval should be. This is done by binding the parameter T. To instantiate an Interval of Integer numbers, one would bind the parameter T to the type Integer. Thus, the incomplete data type Interval is completed to the data type Interval of Integer.
For example the following type definition for MyType declares a property named "multiplicity" that is an interval of the cardinal number data type used in the above examples.
|
1.9.5.1
Generic Collections
Generic data types for collections are being used throughout this specification. The most important of them are
Set (SET<T>) A set contains elements in no particular order and without duplicate elements.
Sequence (LIST<T>) A sequence is a collection of values in an arbitrary but particular order. A sequence has a head and a tail, where the head is an element and the tail is the sequence without its head.
Interval (IVL<T>) An interval is a continuous subset of an ordered type.
These and other generic types are fully defined in Generic Data Types (§ 1.9.5 ). These generic data types and their properties are being used in this specification early on. For the best understanding of this specification knowledge about the set, sequence and interval is important and the reader is advised to refer to Generic Data Types (§ 1.9.5 ). when coming across a generic type being used to define another type.
1.9.5.2
Generic Type Extensions
Generic data type extensions are generic types with one parameter type that the generic type specializes. In the formal data type definition language, generic type specializations follow the pattern:
|
These generic type extensions inherit properties of their base type and add some specific feature to it. The generic type extension is a specialization of the base type, thus a value of the extension data type can be used instead of its base data type.15
NOTE: Values of extended types can be substituted for their base type. However, an ITS may make some constraints as to what extensions to accommodate. Particularly, extensions need not be defined for those components carrying the values of data value properties. Thus, while any data value can be annotated outside the data type specification, an ITS may not provide for a way to annotate the value of a data value property.

Fundamental data types
1.10
Conformance
If an application receives or parses an instance that is not valid with regard to this specification, the receiver is permitted to reject the instance in whatever fashion it deems appropriate but it is not required to. Note that some other HL7 standard or artefact such as a conformance statement may make additional constraints on behaviour in such cases.
1.11
DataValue (ANY)
Definition: Defines the basic properties of every data value. This is an abstract type, meaning that no value can be just a data value without belonging to any concrete type. Every concrete type is a specialization of this general abstract DataValue type.
|
1.11.1
Data Type : TYPE
Definition: Represents the fact that every data value implicitly carries information about its own data type. Thus, given a data value one can inquire about its data type.
|
1.11.2
Proper Value : BN
Definition: Indicates that a value is a non-exceptional value of the data type.
|
When a property, RIM attribute, or message field is called mandatory this means that any non-NULL value of the type to which the property belongs has a non-NULL value for that property, in other words, a field may not be NULL, providing that its container (object, segment, etc.) is to have a non-NULL value.
1.11.3
Exceptional Value : BN
Definition: Indicates that a value is an exceptional value, or a NULL-value. A null value means that the information does not exist, is not available or cannot be expressed in the data type's normal value set.
Every data element has either a proper value or it is considered NULL. If (and only if) it is NULL, the isNull provides more detail as to in what way or why no proper value is supplied.
|
1.11.4
Exceptional Value Detail : CS
Definition: If a value is an exceptional value (NULL-value), this specifies in what way and why proper information is missing.
|
The null flavors are a general domain extension of all normal data types. Note the distinction between value domain of any data type and the vocabulary domain of coded data types. A vocabulary domain is a value domain for coded values, but not all value domains are vocabulary domains.
The null flavor "other" is used whenever the actual value is not in the required value domain, this may be, for example, when the value exceeds some constraints that are defined too restrictive (e.g., age less than 100 years.)
NOTE: NULL-flavors are applicable to any property of a data value or a higher-level object attribute. Where the difference of null flavors is not significant, ITS are not required to represent them. If nothing else is noted in this specification, ITS need not represent general NULL-flavors for data-value properties.
Some of these null flavors are associated with named properties that can be used as simple predicates for all data values. This is done to simplify the formulation of invariants in the remainder of this specification.
Remember the difference between semantic properties and representational "components" of data values. An ITS must only represent those components that are needed to infer the semantic properties. The null-flavor predicates nonNull, isNull, notApplicable, unknown, and other can all be inferred from the nullFlavor property.
1.11.5
Inapplicable Proper Value : BL
Definition: A predicate indicating that this exceptional value is of nullFlavor not-applicable (NA), i.e., that a proper value is not meaningful in the given context.
|
1.11.6
unknown : BL
Definition: A predicate indicating that this exceptional value is of nullFlavor unknown (UNK).
|
1.11.7
Value Domain Exception : BL
Definition: A predicate indicating that this exceptional value is of nullFlavor other (OTH), i.e., that the required value domain does not contain the appropriate value.
|
1.11.8
Equality : BL
Definition: Equality is a reflexive, symmetric, and transitive relation between any two data values. Only proper values can be equal, null values never are equal (even if they have the same null flavor.)
|
How equality is determined must be defined for each data type. If nothing else is specified, two data values are equal if they are indistinguishable, that is, if they differ in none of their semantic properties. A data type can "override" this general definition of equality, by specifying its own equal relationship. This overriding of the equality relation can be used to exclude semantic properties from the equality test. If a data type excludes semantic properties from its definition of equality, this implies that certain properties (or aspects of properties) that are not part of the equality test are not essential to the meaning of the value.
For example the physical quantity has the two semantic properties (1) a real number and (2) a coded unit of measure. The equality test, however, must account for the fact that, e.g., 1 meter equals 100 centimeters; independent equality of the two semantic properties is too strong a criterion for the equality test. Therefore, physical quantity must override the equality definition.
1.12
DataType (TYPE) specializes ANY
Definition: A meta-type declared in order to allow the formal definitions to speak about the data type of a value. Any data type defined in this specification is a value of the type DataType.
|
1.12.1
Short Name : CS
Definition: A CS specifying the alias of the data type.
|
1.12.2
Long Name : CS
Definition: A CS specifying the full name of the data type.
1.12.3
Implies : BN
Definition: A data type implies another data type if it has the same type or is a specialisation of it.
2
Basic Types
2.1
Boolean (BL) specializes ANY
Definition: BL stands for the values of two-valued logic. A BL value can be either true or false, or, as any other value may be NULL.
|
With any data value potentially being NULL, the two-valued logic is effectively extended to a three-valued logic as shown in the following truth tables:
Where a boolean operation is performed upon 2 data types with different nullFlavors, the nullFlavor of the result is the first common ancestor of the 2 different nullFlavors, though conformant applications may also create a result that is any common ancestor
2.1.1
Negation : BL
Definition: Negation of a BL turns true into false and false into true and is NULL for NULL values.
|
2.1.2
Conjunction : BL
Definition: Conjunction (AND) is associative and commutative, with true as a neutral element. False AND any Boolean value is false. These rules hold even if one or both of the operands are NULL. If both operands for AND are NULL, the result is NULL.
|
2.1.3
Disjunction : BL
Definition: The disjunction x OR y is false if and only if x is false and y is false.
|
2.1.4
Exclusive Disjunction : BL
Definition: The exclusive-OR constrains OR such that the two operands may not both be true.
|
2.1.5
Implication : BL
Definition: A rule of the form IF condition THEN conclusion. Logically the implication is defined as the disjunction of the negated condition and the conclusion, meaning that when the condition is true the conclusion must be true to make the overall statement true. The logical implication is important to make invariant statements.
|
The implication is not reversible and does not specify what is true when the condition is false (ex falso quodlibet lat. “from false follows anything”).
2.1.6
Literal Form
The literal form of the Boolean is determined by the named values specified in the values clause, i.e., true and false.
2.2
BooleanNonNull (BN) specializes BL
Definition: BN constrains the boolean type so that the value may not be NULL. This type is created for use within the data types specification where it is not appropriate for a null value to be used
private type BooleanNonNull alias BN specializes BL; }; |
2.2.1
isNull : BN
|
2.3
Binary Data (BIN) specializes LIST<BN>
Definition: BIN is a raw block of bits. BIN is a protected type that should not be declared outside the data type specification.
A bit is semantically identical with a non-null BL value. Thus, all binary data is — semantically — a sequence of non-null BL values.
protected type BinaryData alias BIN specializes LIST<BN>; |
NOTE: The representation of arbitrary binary data is the responsibility of an ITS. How the ITS accomplishes this depends on the underlying Implementation Technology (whether it is character-based or binary) and on the represented data. Semantically character data is represented as binary data, however, a character-based ITS should not convert character data into arbitrary binary data and then represent binary data in a character encoding. Ultimately even character-based implementation technology will communicate binary data.
An empty sequence is not considered binary data but counts as a NULL-value. In other words, non-NULL binary data contains at least one bit. No bit in a non-NULL binary data value can be NULL.
|
2.4
Encapsulated Data (ED) specializes BIN
Definition: Data that is primarily intended for human interpretation or for further machine processing outside the scope of HL7. This includes unformatted or formatted written language, multimedia data, or structured information in as defined by a different standard (e.g., XML-signatures.) Instead of the data itself, an ED may contain only a reference (see TEL.) Note that ST is a specialization of the ED where the mediaType is fixed to text/plain.
| Name | Type | Description |
|---|---|---|
| mediaType | CS | Identifies the type of the encapsulated data and identifies a method to interpret or render the data. |
| charset | CS | For character-based encoding types, this property specifies the character set and character encoding used. The charset shall be identified by an Internet Assigned Numbers Authority (IANA) Charset Registration [http://www.iana.org/assignments/character-sets] in accordance with RFC 2978 [http://www.ietf.org/rfc/rfc2978.txt]. |
| language | CS | For character based information the language property specifies the human language of the text. |
| compression | CS | Indicates whether the raw byte data is compressed, and what compression algorithm was used. |
| reference | TEL | A telecommunication address (TEL), such as a URL for HTTP or FTP, which will resolve to precisely the same binary data that could as well have been provided as inline data. |
| integrityCheck | BIN | The integrity check is a short binary value representing a cryptographically strong checksum that is calculated over the binary data. The purpose of this property, when communicated with a reference is for anyone to validate later whether the reference still resolved to the same data that the reference resolved to when the encapsulated data value with reference was created. |
| integrityCheckAlgorithm | CS |
Specifies the algorithm used to compute the integrityCheck
value.
The cryptographically strong checksum algorithm Secure Hash Algorithm-1 (SHA-1) is currently the industry standard. It has superseded the MD5 algorithm only a couple of years ago, when certain flaws in the security of MD5 were discovered. Currently the SHA-1 hash algorithm is the default choice for the integrity check algorithm. Note that SHA-256 is also entering widespread usage. |
| thumbnail | ED | An abbreviated rendition of the full data. A thumbnail requires significantly fewer resources than the full data, while still maintaining some distinctive similarity with the full data. A thumbnail is typically used with by-reference encapsulated data. It allows a user to select data more efficiently before actually downloading through the reference. |
Encapsulated data can be present in two forms, inline or by reference. Inline data is communicated or moved as part of the encapsulated data value, whereas by-reference data may reside at a different (remote) location. The data is the same whether it is located inline or remote.
2.4.1
Media Type : CS
Definition: Identifies the type of the encapsulated data and identifies a method to interpret or render the data.
mediaType is a mandatory property, i.e., every non-NULL instance of ED must have a non-NULL mediaType property.
|
The IANA defined domain of media types is established by the Internet standard RFC 2045 [http://www.ietf.org/rfc/rfc2045.txt] and 2046 [http://www.ietf.org/rfc/rfc2046.txt]. RFC 2046 defines the media type to consist of two parts:
- top level media type, and
- media subtype
However, this specification treats the entire media type as one atomic code symbol in the form defined by IANA, i.e., top level type followed by a slash "/" followed by media subtype. Currently defined media types are registered in a database [http://www.iana.org/assignments/media-types/index.html] maintained by IANA. Currently more than 160 different MIME media types are defined, with the list growing rapidly. In general, all those types defined by the IANA may be used.
To promote interoperability, this specification prefers certain media types to others. This is to define a greatest common denominator on which interoperability is not only possible, but that is powerful enough to support even advanced multimedia communication needs.
Table 6 below assigns a status to certain MIME media types, where the status means one of the following:
- required: Every HL7 application must support at least the required media types if it supports a given kind of media. One required media-type for each kind of media exists. Some media types are required for a specific purpose, which is then indicated as "required for ..."
- recommended: Other media types are recommended for a particular purpose. For any given purpose there should be only very few additionally recommended media types and the rationale, conditions and assumptions of such recommendations must be made very clear.
- indifferent: This status means, HL7 neither forbids nor endorses the use of this media type. All media types not mentioned in Table 6 have status indifferent by default. Since there is one required and several recommended media types for most practically relevant use cases, media types of this status should be used very conservatively.
- deprecated: Deprecated media types should not be used, because these media types are flawed, because there are better alternatives, or because of certain risks. Such risks could be security risks, for example, the risk that such a media type could spread computer viruses. Not every flawed media type is marked as deprecated, though. A media type that is not mentioned in Table 6, and thus has status indifferent, may well be flawed.
The set of required media types is very small so that no undue requirements are forced on HL7 applications, especially legacy systems. In general, no HL7 application is forced to support any given kind of media other than written text. For example, many systems just do not want to receive audio data, because those systems can only show written text to their users. It is a matter of application conformance statements to say: "I will not handle audio". Only if a system claims to handle audio media, it must support the required media type for audio.
2.4.2
Charset : CS
Definition: For character-based encoding types, this property specifies the character set and character encoding used. The charset shall be identified by an Internet Assigned Numbers Authority (IANA) Charset Registration [http://www.iana.org/assignments/character-sets] in accordance with RFC 2978 [http://www.ietf.org/rfc/rfc2978.txt].
The charset domain is maintained by the Internet Assigned Numbers Authority (IANA) [http://www.iana.org/assignments/character-sets]. The IANA source specifies names and multiple aliases for most character sets. For HL7's purposes, use of multiple alias names is not allowed. The standard name for HL7 is the one marked by IANA as "preferred for MIME." If IANA has not marked one of the aliases as "preferred for MIME" the main name shall be the one used for HL7.
Table 7 lists a few of the IANA defined character sets that are of interest to current HL7 members.
NOTE: The above list is not complete let alone exclusive. In particular, international HL7 affiliates may make special recommendations about charsets to be used in their realm. These recommendations may add additional charsets and may reassign the recommendations status of a listed charset.
The charset property needs to be known where the data of the ED is character type data in any form. If the data is provided in-line, then the charset must be known. If the data is provided as a reference, and the access method does not provide the charset for the data, typically as a mime header, then the charset must be conveyed as part of the ED.
Interested readers may also want to consult the "Character Model for the World Wide Web" [http://www.w3.org/TR/charmod] for a more complete discussion of character set and related issues
2.4.3
Language : CS
Definition: For character based information the language property specifies the human language of the text.
The need for a language code for text data values is documented in RFC 2277, IETF Policy on Character Sets and Languages [http://www.ietf.org/rfc/rfc2277.txt]. Further background information can be found in Using International Characters in Internet Mail [http://www.imc.org/mail-i18n.html], a memo by the Internet Mail Consortium.
The principles of the code domain of this attribute are specified by the Internet standard RFC 3066 [http://www.ietf.org/rfc/rfc3066.txt]. The RFC 3066 coding scheme is constructed from a primary subtag component encoded using the language codes of ISO 639, plus two codes for extensions for languages not represented in ISO 639. The code optionally includes a second subtag component encoded using the two letter country codes of ISO 3166, or a language code extension registered by the Internet Assigned Names Authority [http://www.iana.org/assignments/language-tags].17
While Language tags usually alter the meaning of the text, the language does not alter the meaning of the characters in the text.18
NOTE: Representation of language tags to text is highly dependent on the ITS. An ITS may use the native way of language tagging provided by its target implementation technology. Some may have language information in a separate component, e.g., XML has the xml:lang tag for strings. Others may rely on language tags as part of the binary character string representation, e.g., ISO 10646 (Unicode) and its "plane-14" language tags.
The language tag should not be mandatory if it is not mandatory in the implementation technology. Semantically, language tagging of strings follows a default-logic. In circumstances where a realm may support multiple langauges, it is up to the realm to define rules to handle language where none is specified when no language is specified. If no other rule is specified, the local language of the reader is assumed. If a language is set for an entire message or document, that language is the default. If any information element or value that is superior in the syntax hierarchy specifies a language, that language is the default for all subordinate text values.
If language tags are present in the beginning of the encoded binary text (e.g., through Unicode's plane-14 tags) this is the source of the language property of the encapsulated data value.
2.4.4
Compression : CS
Definition: Indicates whether the raw byte data is compressed, and what compression algorithm was used.
Values of type ST may never be compressed.
2.4.5
Reference : TEL
Definition: A telecommunication address (TEL), such as a URL for HTTP or FTP, which will resolve to precisely the same binary data that could as well have been provided as inline data.
The semantic value of an encapsulated data value is the same, regardless whether the data is present inline data or just by-reference. However, an encapsulated data value without inline data behaves differently, since any attempt to examine the data requires the data to be downloaded from the reference. An encapsulated data value may have both inline data and a reference.
The reference must point to the same data as provided inline. It is an error if the data resolved through the reference does not match either the integrity check, in-line data, or data that had earlier been retrieved through the reference and then cached.
The reference may contain a usablePeriod to indicate that the data may only be available for a limited period of time. Whether the reference is limited by a usablePeriod or not, the content of the reference is fixed for all time. Any application using the reference must always receive the same data. The reference cannot be reused to send a different version of the same data, or different data.
By-reference encapsulated data may not be allowed depending on the attribute or component that is declared encapsulated data. Values of type ST must always be inline.
2.4.6
Integrity Check : BIN
Definition: The integrity check is a short binary value representing a cryptographically strong checksum that is calculated over the binary data. The purpose of this property, when communicated with a reference is for anyone to validate later whether the reference still resolved to the same data that the reference resolved to when the encapsulated data value with reference was created.
It is an error if the data resolved through the reference does not match the integrity check.
The integrity check is calculated according to the integrityCheckAlgorithm. By default, the Secure Hash Algorithm-1 (SHA-1) shall be used. The integrity check is binary encoded according to the rules of the integrity check algorithm.
The integrity check is calculated over the raw binary data that is contained in the data component, or that is accessible through the reference. No transformations are made before the integrity check is calculated. If the data is compressed, the Integrity Check is calculated over the compressed data.
2.4.7
Integrity Check Algorithm : CS
Definition: Specifies the algorithm used to compute the integrityCheck value.19
2.4.8
Thumbnail : ED
Definition: An abbreviated rendition of the full data. A thumbnail requires significantly fewer resources than the full data, while still maintaining some distinctive similarity with the full data. A thumbnail is typically used with by-reference encapsulated data. It allows a user to select data more efficiently before actually downloading through the reference.
Originally, the term thumbnail refers to an image in a lower resolution (or smaller size) than another image. However, the thumbnail concept can be metaphorically used for media types other than images. For example, a movie may be represented by a shorter clip; an audio-clip may be represented by another audio-clip that is shorter, has a lower sampling rate, or a lossy compression.
Thumbnails may not be allowed depending on the attribute or component that is declared encapsulated data. Values of type ST never have thumbnails, and a thumbnail may not itself contain a thumbnail.
|
NOTE: ITS's should consider the case where the thumbnail and the original both have the same properties of type, charset and compression. In this case, these properties need not be represented explicitly for the thumbnail but might be "inherited" from the main encapsulated data value to its thumbnail.
2.4.9
Equality : BL, inherited from ANY
Two values of type ED are equal if and only if their mediatype and data are equal. For those ED values with compressed data or referenced data, only the de-referenced and uncompressed data counts for the equality test. The compression, thumbnail and reference property themselves are excluded from the equality test. In addition the language property is excluded from the test, due to the problems this would introduce values of type ED where the language is not specified. If the mediaType is character based and the charset property is not equal, the charset property must be resolved through mapping of the data between the different character sets.
The integrity check algorithm and integrity check is excluded from the equality test. However, since equality of integrity check value is strong indication for equality of the data, the equality test can be practically based on the integrity check, given equal integrity check algorithm properties.
2.5
Character String (ST) specializes ED
Definition: The character string data type stands for text data, primarily intended for machine processing (e.g., sorting, querying, indexing, etc.) Used for names, symbols, and formal expressions.
ST is a restricted ED, whose ED.mediaType property is fixed to text/plain, and whose data must be inlined and not compressed. Thus, the properties compression, reference, integrity check, algorithm, and thumbnail are not applicable. The character string data type is used when the appearance of text does not bear meaning, which is true for formalized text and all kinds of names.
| Name | Type | Description |
|---|---|---|
| mediaType | CS | Identifies the type of the encapsulated data and identifies a method to interpret or render the data. |
| charset | CS | For character-based encoding types, this property specifies the character set and character encoding used. The charset shall be identified by an Internet Assigned Numbers Authority (IANA) Charset Registration [http://www.iana.org/assignments/character-sets] in accordance with RFC 2978 [http://www.ietf.org/rfc/rfc2978.txt]. |
| language | CS | For character based information the language property specifies the human language of the text. |
ST data type interprets the encapsulated data as character data (as opposed to bits), depending on the charset property of the encapsulated data type.
|
NOTE: Because many of the properties of the encapsulated data are bound to a default value, an ITS need not represent these properties at all. In fact, if the character encoding is also fixed, the ITS only represents the encoded character data.
The headCharacter and tailString properties define ST as a sequence of entities each of which uniquely identifies one character from the joint set of all characters known by any language of the world.20
The head of an ST is a string of only one character. An ST must have at least one character or else it is NULL. A zero-length ST is an exceptional value (NULL), not a proper value.
|
The length of an ST is the number of characters, not the number of encoded bytes, in the string. Byte encoding is an ITS issue and is not relevant on the application layer.
The following rules apply to whitespace contained within values of type ST:
- TAB, space and end-of-line are all considered whitespace characters.
- Both preceding and trailing whitespace is significant.
- Different whitespace characters are not interchangable.
- Different representations of end-of-line are normalised according to the method described in the XML specification [Section 2.11 End-of-Line Handling]
- Sequences of whitespace cannot be compressed to shorter sequences.
| Requirement ST is a specialization of ED so that any RIM attribute which has the type ED can be constrained to a ST. The most important case is Act.text, which is an ED to cater for the use of references and multimedia data, but is often constrained to plain text. |
2.5.1
Media Type : CS, inherited from ED
|
Fixed to be "text/plain".
2.5.2
Charset : CS, inherited from ED
|
Values of type ST must have a known charset.
2.5.3
Language : CS, inherited from ED
Definition: For character based information the language property specifies the human language of the text.
The need for a language code for text data values is documented in RFC 2277, IETF Policy on Character Sets and Languages [http://www.ietf.org/rfc/rfc2277.txt]. Further background information can be found in Using International Characters in Internet Mail [http://www.imc.org/mail-i18n.html], a memo by the Internet Mail Consortium.
The principles of the code domain of this attribute are specified by the Internet standard RFC 3066 [http://www.ietf.org/rfc/rfc3066.txt]. The RFC 3066 coding scheme is constructed from a primary subtag component encoded using the language codes of ISO 639, plus two codes for extensions for languages not represented in ISO 639. The code optionally includes a second subtag component encoded using the two letter country codes of ISO 3166, or a language code extension registered by the Internet Assigned Names Authority [http://www.iana.org/assignments/language-tags].21
While Language tags usually alter the meaning of the text, the language does not alter the meaning of the characters in the text.22
NOTE: Representation of language tags to text is highly dependent on the ITS. An ITS may use the native way of language tagging provided by its target implementation technology. Some may have language information in a separate component, e.g., XML has the xml:lang tag for strings. Others may rely on language tags as part of the binary character string representation, e.g., ISO 10646 (Unicode) and its "plane-14" language tags.
The language tag should not be mandatory if it is not mandatory in the implementation technology. Semantically, language tagging of strings follows a default-logic. In circumstances where a realm may support multiple langauges, it is up to the realm to define rules to handle language where none is specified when no language is specified. If no other rule is specified, the local language of the reader is assumed. If a language is set for an entire message or document, that language is the default. If any information element or value that is superior in the syntax hierarchy specifies a language, that language is the default for all subordinate text values.
If language tags are present in the beginning of the encoded binary text (e.g., through Unicode's plane-14 tags) this is the source of the language property of the encapsulated data value.
2.5.4
Compression : CS, (fixed)
|
Values of type ST cannot be compressed.
2.5.5
Reference : TEL, (fixed)
|
Values of type ST may not reference content from some other location.
2.5.6
Integrity Check : BIN, (fixed)
|
Integrity check code is not used with values of type ST.
2.5.7
Integrity Check Algorithm : CS, (fixed)
|
Integrity check algorithm is not used with values of type ST.
2.5.8
Thumbnail : ED, (fixed)
|
Values of type ST do not have thumbnails.
2.5.9
Literal Form
Two variations of ST literals are defined, a token form and a quoted string.23 The token form consists only of the lower case and upper case Latin alphabet, the ten decimal digits and the underscore. The quoted string can contain any character between double-quotes. The double quotes prevent a character string from being interpreted as some other literal. The token form allows keywords and names to be parsed from the data type specification language.
|
NOTE: Since ST literals are so fundamental to implementation technology, most ITS will specify some modified character string literal form. However, ITS designers must be aware of the interaction between the ST literal form and the literal forms defined for other data types. This is particularly critical if the other data type's literal form is structured with major components separated by break-characters (e.g., real number, physical quantity, set, and list literals, etc.)
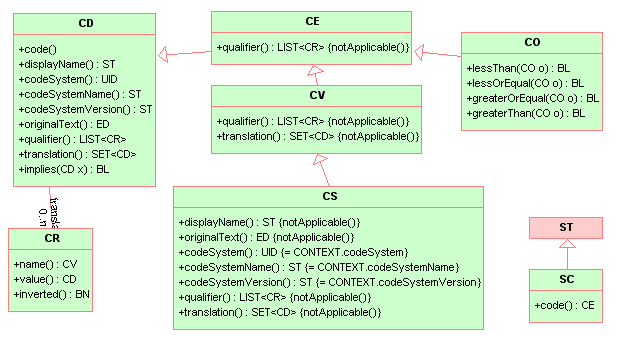
The Concept Descriptor information model.
2.6
Concept Descriptor (CD) specializes ANY
Definition: A CD represents any kind of concept usually by giving a code defined in a code system. A CD can contain the original text or phrase that served as the basis of the coding and one or more translations into different coding systems. A CD can also contain qualifiers to describe, e.g., the concept of a "left foot" as a postcoordinated term built from the primary code "FOOT" and the qualifier "LEFT". In cases of an exceptional value, the CD need not contain a code but only the original text describing that concept.
CD is mostly used in one of its restricted or "profiled" forms, CS, CE, CV. Use of the full concept descriptor data type is not common. It requires a conscious decision and documented rationale. In all other cases, one of the CD restrictions shall be used.24
All CD restrictions constrain certain properties. Properties may be constrained to the extent that only one value may be allowed for that property, in which case mentioning the property becomes redundant. Constraining a property to one value is referred to as suppressing that property. Although, conceptually a suppressed property is still semantically applicable, it is safe for an HL7 interface to assume the implicit default value without testing.
NOTE: In general, this is true of many types in this data types specification, however it is a frequently asked question concerning the CD descendents.
2.6.1
Code : ST
Definition: The plain code symbol defined by the code system. For example, "784.0" is the code symbol of the ICD-9 code "784.0" for headache.
A non-exceptional CD value has a non-NULL code property whose value is a character string that is a symbol defined by the coding system identified by codeSystem. Conversely, a CD value without a value for the code property, or with a value that is not from the cited coding system is an exceptional value (NULL of flavor other).
|
2.6.2
Code System : UID
Definition: Specifies the code system that defines the code.
Code systems shall be referred to by a UID, which allows unambiguous reference to standard HL7 codes, other standard code systems, as well as local codes. HL7 shall assign a UID to each of its code tables as well as to external standard coding systems that are being used with HL7. Local sites must use their ISO Object Identifier (OID) to construct a globally unique local coding system identifier.
Under HL7's branch, 2.16.840.1.113883, the sub-branches 5 and 6 contain HL7 standard and external code system identifiers respectively. The HL7 Vocabulary Technical Committee maintains these two branches.
A non-exceptional CD value (i.e. a CD value that has a non-null code property) has a non-NULL codeSystem specifying the system of concepts that defines the code. In other words whenever there is a code there is also a code system.
NOTE: Although every non-NULL CD value has a defined code system, in some circumstances, the ITS representation for the CD value needs not explicitly mention the code system. For example, when the context mandates one and only one code system to be used specifying the code system explicitly would be redundant. However, in that case the codeSystem takes on that context-specific default value and is not NULL.
|
An exceptional CD of NULL-flavor other indicates that a concept could not be coded in the coding system specified. Thus, for these coding exceptions, the code system that did not contain the appropriate concept must be provided in codeSystem.
Some code domains are qualified such that they include the portion of any pertinent local coding system that does not simply paraphrase the standard coding system (coded with extensibility, CWE.) If a CWE qualified field actually contains such a local code, the coding system must specify the local coding system from which the local code was taken. However, for CWE domains the local code is a valid member of the domain, so that local codes in CWE domains constitute neither an error nor an exceptional (NULL/other) value in the sense of this specification.
|
2.6.3
Code System Name : ST
Definition: The common name of the coding system.
The code system name has no computational value. The purpose of a code system name is to assist an unaided human interpreter of a code value to interpret codeSystem. It is suggested — though not absolutely required — that ITS provide for codeSystemName in order to annotate the UID for human comprehension.
HL7 systems must not functionally rely on codeSystemName. codeSystemName can never modify the meaning of codeSystem and cannot exist without codeSystem.
|
2.6.4
Code System Version : ST
Definition: If applicable, a version descriptor defined specifically for the given code system.
HL7 shall specify how these version strings are formed for each external code system. If HL7 has not specified how version strings are formed for a particular coding system, version designations have no defined meaning for such coding system.
Different versions of one code system must be compatible. Whenever a code system changes in an incompatible way, it will constitute a new code system, not simply a different version, regardless of how the vocabulary publisher calls it.
For example, the publisher of ICD-9 and ICD-10 calls these code systems, "revision 9" and "revision 10" respectively. However, ICD-10 is a complete redesign of the ICD code, not a backward compatible version. Therefore, for the purpose of this data type specification, ICD-9 and ICD-10 are different code systems, not just different versions. By contrast, when LOINC updates from revision "1.0j" to "1.0k", HL7 would consider this to be just another version of LOINC, since LOINC revisions are backwards compatible.
|
2.6.5
Display Name : ST
Definition: A name or title for the code, under which the sending system shows the code value to its users.
displayName is included both as a courtesy to an unaided human interpreter of a code value and as a documentation of the name used to display the concept to the user. The display name has no functional meaning; it can never exist without a code; and it can never modify the meaning of code.
NOTE: HL7 offers a "print name" in it's predefined vocabulary domains. These values are suitable for use in the displayName.
NOTE: Display names may not alter the meaning of the code value. Therefore, display names should not be presented to the user on a receiving application system without ascertaining that the display name adequately represents the concept referred to by the code value. Communication must not simply rely on the display name. The display name's main purpose is to support debugging of HL7 protocol data units (e.g., messages.)
|
2.6.6
Original Text : ED
Definition: The text or phrase used as the basis for the coding.
The original text exists in a scenario where an originator of the information does not assign a code, but where the code is assigned later by a coder (post-coding.) In the production of a concept descriptor, original text may thus exist without a code.
NOTE: Although post-coding is often performed from free text information, such as documents, scanned images or dictation, multi-media data is explicitly not permitted as original text. Also, the original text property is not meant to be a link into the entire source document. The link between different artifacts of medical information (e.g., document and coded result) is outside the scope of this specification and is maintained elsewhere in the HL7 standards. The original text is an excerpt of the relevant information in the original sources, rather than a pointer or exact reproduction. Thus the original text is to be represented in plain text form.
Values of type CD may have a non-NULL original text property despite having a NULL code. Any CD value with code of NULL signifies a coding exception. In this case, originalText is a name or description of the concept that was not coded. Such exceptional CD values may also contain translations. Such translations directly encode the concept described in originalText.
A CD can be demoted into an ST value representing only the originalText of the CD value.
|
2.6.7
Translation : SET<CD>
Definition: A set of other concept descriptors that translate this concept descriptor into other code systems.
translation is a set of other CDs that each translate the first CD into different code systems. Each element of the translation set was translated from the first CD. Each translation may, however, also contain translations. Thus, when a code is translated multiple times the information about which code served as the input to which translation will be preserved.
NOTE: The translations are quasi-synonyms of one real-world concept. Every translation in the set is supposed to express the same meaning "in other words." However, exact synonymy rarely exists between two structurally different coding systems. For this reason, not all of the translations will be equally exact.
2.6.8
Qualifier : LIST<CR>
Definition: Specifies additional codes that increase the specificity of the the primary code.
The primary code and all the qualifiers together make up one concept. A CD with qualifiers is also called a code phrase or postcoordinated expression.
Qualifiers constrain the meaning of the primary code, but cannot negate it or change it's meaning to that of another value in the primary coding system
Qualifiers can only be used according to well-defined rules of post-coordination. A value of type CD may only have qualifiers if it's code system defines the use of such qualifiers or if there is a third code system that specifies how other code systems may be combined.
For example, SNOMED CT allows constructing concepts as a combination of multiple codes. SNOMED CT defines a concept "cellulitis (disorder)" (128045006) an attribute "finding site" (363698007) and another concept "foot structure (body structure)" (56459004). SNOMED CT allows one to combine these codes in a code phrase:
<observation>
...
<value code="128045006" codeSystem="&SNOMED-CT;" displayName="cellulitis (disorder)">
<qualifier code="56459004" displayName="foot structure">
<name code="363698007" displayName="finding site"/>
</qualifier>
</value>
...
</observation> |
In this example, there is one code system, SNOMED-CT that defines the primary code and all the qualifiers and how these are used, which is why in our example representation the codeSystem does not need to be mentioned for the qualifier name and value (the codeSystem is inherited from the primary code.)
It is important to note that the allowable qualifiers are specified by the code system. For instance, in SNOMED CT, there is a defined set of qualifying attributes, and only Findings and Disorders can be qualified with the "finding site" attribute. Use of qualifiers outside the boundaries specified by the code system is a non-conformant use of the CD data type. Adherence to the rules specified by the code system enables post-coordinated expressions to be compared with pre-coordinated concepts (such as where one might compare the above code phrase to the pre-coordinated concept "cellulitis of foot (disorder)" (128276007), which is defined within SNOMED CT as having a finding site of foot structure). CD does not provide for normalization of compositional expressions, therefore it is possible to create ambiguous expressions. Users should understand that they must provide the additional constraints necessary to assure unambiguous data representation, if they are planning to create compositional expressions using CD. Otherwise, they risk the inability to retrieve a complete set of all records corresponding to any given query.
Another common example is the U.S. Centers for Medicare and Medicaid Services (CMS) (previously known as the Health Care Financing Administration, HCFA) procedure codes. CMS procedure codes (HCPCS) are based on CPT-4 and add additional qualifiers to it. For example, the patient with above finding (plus peripheral arterial disease, diabetes mellitus, and a chronic skin lesion at the left great toe) may have an amputation of that toe. The CPT-4 concept is "Amputation, toe metatarsophalangeal joint" (28820) and a HCPCS qualifier needs to be added to indicate "left foot, great toe" (TA). Thus we code:
<procedure>
...
<cd code="28820" codeSystem="&CP4;" displayName="Amputation, toe metatarsophalangeal joint">
<qualifier code="TA" codeSystem="&HCP;" displayName="left foot, great toe"/>
</cd>
...
</procedure> |
In this example, the code system of the qualifier (HCPCS) is different than the code system of the primary code (CPT-4.) It is only because there are well-defined rules that define how these codes can be combined, that the qualifier may be used. Note also, that the role name is optional, and for HCPCS codes there are no distinguished role names.
The order of qualifiers is preserved, particularly for the case where the coding system allows post-coordination but defines no role names. (e.g., some ICD-9CM codes, or the old SNOMED "multiaxial" coding.)
2.6.9
Equality : BL, inherited from ANY
The main use of concept descriptors is for the purpose of indexing, querying and decision-making based on a coded value. A semantically unambiguous specification of coded values therefore requires a clear definition of what equality of concept descriptor values means and how CD values should be compared. (For more details on comparing pre- and post-coordinated expressions, see Dolin RH, Spackman KA, Markwell D. Selective Retrieval of Pre- and Post-coordinated SNOMED Concepts. Fall AMIA 2002; 210-14, or the July 2003 SNOMED CT Implementation Guide.)
The equality of two CD values is determined solely based upon code and codeSystem. codeSystemVersion is excluded from the equality test.25 If qualifiers are present, the qualifiers are included in the equality test. Translations are not included in the equality test.26 Exceptional CD values are not equal even if they have the same NULL-flavor or the same original text.27
|
Some code systems define certain style options to their code values. For example, the U.S. National Drug Code (NDC) has a dash and a non-dash form. An example for the dash form may be 1234-5678-90 when the non-dash form is 01234567890. Another example for this problem is when certain ISO or ANSI code tables define optional alphanumeric and numeric forms of two or three character lengths all in one standard.
In the case where code systems provide for multiple representations, HL7 shall make a ruling about which is the preferred form. HL7 shall document that ruling where that respective external coding system is recognized. HL7 shall decide upon the preferred form based on criteria of practicality and common use. In absence of clear criteria of practicality and common use, the safest, most extensible, and least stylized (the least decorated) form shall be given preference.28
2.6.10
Implies : BL
Definition: Specifies whether this CD is a specialization of the operand CD.
Naturally, concepts can be narrowed and widened to include or exclude other concepts. Many coding systems have an explicit notion of concept specialization and generalization. The HL7 vocabulary principles also provide for concept specialization for HL7 defined value sets. implies is a predicate that compares whether one concept is a specialization of another concept, and therefore implies that other concept.
When writing predicates (e.g., conditional statements) that compare two codes, one should usually test for implication not equality of codes.
For example, in Table 20 the "telecommunication use" concepts: work (W), home (H), primary home (HP), and vacation home (HV) are defined, where both HP and HV imply H. When selecting any home phone number, one should test whether the given use-code c implies H. Testing for c equal H would only find unspecified home phone numbers, but not the primary home phone number.
Operationally, implication can be evaluated in one of two ways. The code system literals may be designed such that one single hierarchy is reflected in the code literal itself (e.g., ICD-9.) Apart from such special cases, however, a terminological knowledge base and an appropriate subsumption algorithm will be required to evaluate implication statements. For post-coordinated coding systems, designing such a subsumption algorithm is a non-trivial task.29
2.7
Concept Role (CR) specializes ANY
Definition: A concept qualifier code with optionally named role. Both qualifier role and value codes must be defined by the coding system of the CD containing the concept qualifier. For example, if SNOMED RT defines a concept "leg", a role relation "has-laterality", and another concept "left", the concept role relation allows to add the qualifier "has-laterality: left" to a primary code "leg" to construct the meaning "left leg".
The use of qualifiers is strictly governed by the code system used. CD does not permit using code qualifiers with code systems that do not provide for qualifiers (e.g. pre-coordinated systems, such as LOINC, ICD-10 PCS.)
|
2.7.1
Name : CV
Definition: Specifies the manner in which the concept role value contributes to the meaning of a code phrase. For example, if SNOMED RT defines a concept "leg", a role relation "has-laterality", and another concept "left", the concept role relation allows to add the qualifier "has-laterality: left" to a primary code "leg" to construct the meaning "left leg". In this example, name is "has-laterality".
If the parent CD.codeSystem allows postcoordination but no role names (e.g. SNOMED) then name can be NULL.
2.7.2
Value : CD
Definition: The concept that modifies the primary code of a code phrase through the role relation. For example, if SNOMED RT defines a concept "leg", a role relation "has-laterality", and another concept "left", the concept role relation allows adding the qualifier "has-laterality: left" to a primary code "leg" to construct the meaning "left leg". In this example, value is "left".
value is of type CD and thus can in turn have qualifiers. This allows qualifiers to nest. Qualifiers can only be used as far as the underlying code system defines them. It is not allowed to use any kind of qualifiers for code systems that do not explicitly allow and regulate such use of qualifiers.
|
2.7.3
Inversion Indicator : BN
Definition: Indicates if the sense of name is inverted. This can be used in cases where the underlying code system defines inversion but does not provide reciprocal pairs of role names. By default, inverted is false.
For example, a code system may define the role relation "causes" and the concepts "Streptococcus pneumoniae" and "Pneumonia". If that code system allows its roles to be inverted, one can construct the post-coordinated concept "Pneumococcus pneumonia" through "Pneumonia - causes, inverted - Streptococcus pneumoniae."
Roles may only be inverted if the underlying coding system allows such inversion. Notably, if a coding system defines roles in inverse pairs or intentionally does not define certain inversions, the appropriate role code (e.g. "caused-by") must be used rather than inversion. It must be known whether the inverted property is true or false, since if it is NULL, the role cannot be interpreted.
NOTE: inverted should be conveyed in an indicator attribute, whose default value is false. That way the inverted indicator does not have to be sent when the role is not inverted.
2.8
Coded Simple Value (CS) specializes CV
Definition: Coded data in its simplest form, where only the code is not predetermined. The code system and code system version are fixed by the context in which the CS value occurs. CS is used for coded attributes that have a single HL7-defined value set.
|
CS can only be used in either of the following cases:
- for a coded attribute which has a single HL7-defined code system, and where code additions to that value set require formal HL7 action (such as harmonization.) Such coded attributes must have type CS.
- for a property in this specification that is assigned to a single code system defined either in this specification or defined outside HL7 by a body that has authority over the concept and the maintenance of that code system.
For example, since ED subscribes to the MIME design, it trusts IETF to manage the media type. This includes that this specification subscribes to the extension mechanism built into the MIME media type code (e.g., "application/x-myapp").
For CS values, the designation of the domain qualifier will always be CNE (coded, non-extensible) and the context will determine which HL7 values to use.30
2.8.1
Code : ST, inherited from CD
|
2.8.2
Code System : UID, (fixed)
Every non-NULL CS value has a defined . The ITS representation of CS need not explicitly mention the code system, because the context mandates one and only one code system to be used. Specifying the code system explicitly would be redundant. However, assumes the context-specific default value and is not NULL.
|
An exceptional CS of NULL-flavor other indicates that a concept could not be coded in the coding system specified. In these cases, code must be Null.
|
2.8.3
Code System Name : ST, (fixed)
|
2.8.4
Code System Version : ST, (fixed)
|
2.8.5
Display Name : ST, (fixed)
|
2.8.6
Original Text : ED, (fixed)
|
2.8.7
Translation : SET<CD>, (fixed)
|
2.8.8
Qualifier : LIST<CR>, (fixed)
|
2.8.9
Literal Form
|
The string literal form of CS is primarily defined for the purposes of this specification. The literal form is a string representation of the code for the codeSystem for the context of the CS. You cannot determine codeSystem or codeSystemVersion from the literal itself, so the literal only has use where the context is known.
2.9
Coded Value (CV) specializes CE
Definition: Coded data, specifying only a code, code system, and optionally display name and original text. Used only as the type of properties of other data types.
|
CV is used when any reasonable use case will require only a single code value to be sent. Thus, it should not be used in circumstances where multiple alternative codes for a given value are desired. This type may be used with both the CNE (coded, non-extensible) and the CWE (coded, with extensibility) domain qualifiers.
2.9.1
Code : ST, inherited from CD
Definition: The plain code symbol defined by the code system. For example, "784.0" is the code symbol of the ICD-9 code "784.0" for headache.
A non-exceptional value has a non-NULL code property whose value is a character string that is a symbol defined by the coding system identified by codeSystem. Conversely, a value without a value for the code property, or with a value that is not from the cited coding system is an exceptional value (NULL of flavor other).
|
2.9.2
Code System : UID, inherited from CD
Definition: Specifies the code system that defines the code.
Code systems shall be referred to by a UID, which allows unambiguous reference to standard HL7 codes, other standard code systems, as well as local codes. HL7 shall assign a UID to each of its code tables as well as to external standard coding systems that are being used with HL7. Local sites must use their ISO Object Identifier (OID) to construct a globally unique local coding system identifier.
Under HL7's branch, 2.16.840.1.113883, the sub-branches 5 and 6 contain HL7 standard and external code system identifiers respectively. The HL7 Vocabulary Technical Committee maintains these two branches.
A non-exceptional value (i.e. a value that has a non-null code property) has a non-NULL codeSystem specifying the system of concepts that defines the code. In other words whenever there is a code there is also a code system.
NOTE: Although every non-NULL value has a defined code system, in some circumstances, the ITS representation for the value needs not explicitly mention the code system. For example, when the context mandates one and only one code system to be used specifying the code system explicitly would be redundant. However, in that case the codeSystem takes on that context-specific default value and is not NULL.
|
An exceptional of NULL-flavor other indicates that a concept could not be coded in the coding system specified. Thus, for these coding exceptions, the code system that did not contain the appropriate concept must be provided in codeSystem.
Some code domains are qualified such that they include the portion of any pertinent local coding system that does not simply paraphrase the standard coding system (coded with extensibility, CWE.) If a CWE qualified field actually contains such a local code, the coding system must specify the local coding system from which the local code was taken. However, for CWE domains the local code is a valid member of the domain, so that local codes in CWE domains constitute neither an error nor an exceptional (NULL/other) value in the sense of this specification.
|
2.9.3
Code System Name : ST, inherited from CD
Definition: The common name of the coding system.
The code system name has no computational value. The purpose of a code system name is to assist an unaided human interpreter of a code value to interpret codeSystem. It is suggested — though not absolutely required — that ITS provide for codeSystemName in order to annotate the UID for human comprehension.
HL7 systems must not functionally rely on codeSystemName. codeSystemName can never modify the meaning of codeSystem and cannot exist without codeSystem.
|
2.9.4
Code System Version : ST, inherited from CD
Definition: If applicable, a version descriptor defined specifically for the given code system.
HL7 shall specify how these version strings are formed for each external code system. If HL7 has not specified how version strings are formed for a particular coding system, version designations have no defined meaning for such coding system.
Different versions of one code system must be compatible. Whenever a code system changes in an incompatible way, it will constitute a new code system, not simply a different version, regardless of how the vocabulary publisher calls it.
For example, the publisher of ICD-9 and ICD-10 calls these code systems, "revision 9" and "revision 10" respectively. However, ICD-10 is a complete redesign of the ICD code, not a backward compatible version. Therefore, for the purpose of this data type specification, ICD-9 and ICD-10 are different code systems, not just different versions. By contrast, when LOINC updates from revision "1.0j" to "1.0k", HL7 would consider this to be just another version of LOINC, since LOINC revisions are backwards compatible.
|
2.9.5
Display Name : ST, inherited from CD
Definition: A name or title for the code, under which the sending system shows the code value to its users.
displayName is included both as a courtesy to an unaided human interpreter of a code value and as a documentation of the name used to display the concept to the user. The display name has no functional meaning; it can never exist without a code; and it can never modify the meaning of code.
NOTE: HL7 offers a "print name" in it's predefined vocabulary domains. These values are suitable for use in the displayName.
NOTE: Display names may not alter the meaning of the code value. Therefore, display names should not be presented to the user on a receiving application system without ascertaining that the display name adequately represents the concept referred to by the code value. Communication must not simply rely on the display name. The display name's main purpose is to support debugging of HL7 protocol data units (e.g., messages.)
|
2.9.6
Original Text : ED, inherited from CD
Definition: The text or phrase used as the basis for the coding.
The original text exists in a scenario where an originator of the information does not assign a code, but where the code is assigned later by a coder (post-coding.) In the production of a concept descriptor, original text may thus exist without a code.
NOTE: Although post-coding is often performed from free text information, such as documents, scanned images or dictation, multi-media data is explicitly not permitted as original text. Also, the original text property is not meant to be a link into the entire source document. The link between different artifacts of medical information (e.g., document and coded result) is outside the scope of this specification and is maintained elsewhere in the HL7 standards. The original text is an excerpt of the relevant information in the original sources, rather than a pointer or exact reproduction. Thus the original text is to be represented in plain text form.
Values of type may have a non-NULL original text property despite having a NULL code. Any value with code of NULL signifies a coding exception. In this case, originalText is a name or description of the concept that was not coded. Such exceptional values may also contain translations. Such translations directly encode the concept described in originalText.
A can be demoted into an ST value representing only the originalText of the value.
|
2.9.7
Translation : SET<CD>, (fixed)
|
2.9.8
Qualifier : LIST<CR>, (fixed)
|
2.10
Coded Ordinal (CO) specializes CV
Definition: Coded data, where the coding system from which the code comes is ordered. CO adds semantics related to ordering so that models that make use of such domains may introduce model elements that involve statements about the order of the terms in a domain.
|
The relative order of CO values need not be independently obvious in their literal representation. It is expected that an application will look up the ordering of these values from some table.
2.10.1
Less-or-equal : BL
Definition: The ordering relation is based on lessOrEqual which is taken as primitive in this specification.
All other order relations can be derived from this one. Since lessOrEqual is primitive, this accomodates partial orderings.
Order relationships typically hold only within a single coding system.
2.10.2
Less-than : BL
|
2.10.3
Greater-than : BL
|
2.10.4
Greater-or-equal : BL
|
2.11
Coded With Equivalents (CE) specializes CD
Definition: Coded data that consists of a coded value and, optionally, coded value(s) from other coding systems that identify the same concept. Used when alternative codes may exist.
|
CE is used when the use case indicates that alternative codes may exist and where it is useful to communicate these. CE provides for a primary code value, plus a set of alternative or equivalent representations.
2.11.1
Code : ST, inherited from CD
Definition: The plain code symbol defined by the code system. For example, "784.0" is the code symbol of the ICD-9 code "784.0" for headache.
A non-exceptional value has a non-NULL code property whose value is a character string that is a symbol defined by the coding system identified by codeSystem. Conversely, a value without a value for the code property, or with a value that is not from the cited coding system is an exceptional value (NULL of flavor other).
|
2.11.2
Code System : UID, inherited from CD
Definition: Specifies the code system that defines the code.
Code systems shall be referred to by a UID, which allows unambiguous reference to standard HL7 codes, other standard code systems, as well as local codes. HL7 shall assign a UID to each of its code tables as well as to external standard coding systems that are being used with HL7. Local sites must use their ISO Object Identifier (OID) to construct a globally unique local coding system identifier.
Under HL7's branch, 2.16.840.1.113883, the sub-branches 5 and 6 contain HL7 standard and external code system identifiers respectively. The HL7 Vocabulary Technical Committee maintains these two branches.
A non-exceptional value (i.e. a value that has a non-null code property) has a non-NULL codeSystem specifying the system of concepts that defines the code. In other words whenever there is a code there is also a code system.
NOTE: Although every non-NULL value has a defined code system, in some circumstances, the ITS representation for the value needs not explicitly mention the code system. For example, when the context mandates one and only one code system to be used specifying the code system explicitly would be redundant. However, in that case the codeSystem takes on that context-specific default value and is not NULL.
|
An exceptional of NULL-flavor other indicates that a concept could not be coded in the coding system specified. Thus, for these coding exceptions, the code system that did not contain the appropriate concept must be provided in codeSystem.
Some code domains are qualified such that they include the portion of any pertinent local coding system that does not simply paraphrase the standard coding system (coded with extensibility, CWE.) If a CWE qualified field actually contains such a local code, the coding system must specify the local coding system from which the local code was taken. However, for CWE domains the local code is a valid member of the domain, so that local codes in CWE domains constitute neither an error nor an exceptional (NULL/other) value in the sense of this specification.
|
2.11.3
Code System Name : ST, inherited from CD
Definition: The common name of the coding system.
The code system name has no computational value. The purpose of a code system name is to assist an unaided human interpreter of a code value to interpret codeSystem. It is suggested — though not absolutely required — that ITS provide for codeSystemName in order to annotate the UID for human comprehension.
HL7 systems must not functionally rely on codeSystemName. codeSystemName can never modify the meaning of codeSystem and cannot exist without codeSystem.
|
2.11.4
Code System Version : ST, inherited from CD
Definition: If applicable, a version descriptor defined specifically for the given code system.
HL7 shall specify how these version strings are formed for each external code system. If HL7 has not specified how version strings are formed for a particular coding system, version designations have no defined meaning for such coding system.
Different versions of one code system must be compatible. Whenever a code system changes in an incompatible way, it will constitute a new code system, not simply a different version, regardless of how the vocabulary publisher calls it.
For example, the publisher of ICD-9 and ICD-10 calls these code systems, "revision 9" and "revision 10" respectively. However, ICD-10 is a complete redesign of the ICD code, not a backward compatible version. Therefore, for the purpose of this data type specification, ICD-9 and ICD-10 are different code systems, not just different versions. By contrast, when LOINC updates from revision "1.0j" to "1.0k", HL7 would consider this to be just another version of LOINC, since LOINC revisions are backwards compatible.
|
2.11.5
Display Name : ST, inherited from CD
Definition: A name or title for the code, under which the sending system shows the code value to its users.
displayName is included both as a courtesy to an unaided human interpreter of a code value and as a documentation of the name used to display the concept to the user. The display name has no functional meaning; it can never exist without a code; and it can never modify the meaning of code.
NOTE: HL7 offers a "print name" in it's predefined vocabulary domains. These values are suitable for use in the displayName.
NOTE: Display names may not alter the meaning of the code value. Therefore, display names should not be presented to the user on a receiving application system without ascertaining that the display name adequately represents the concept referred to by the code value. Communication must not simply rely on the display name. The display name's main purpose is to support debugging of HL7 protocol data units (e.g., messages.)
|
2.11.6
Original Text : ED, inherited from CD
Definition: The text or phrase used as the basis for the coding.
The original text exists in a scenario where an originator of the information does not assign a code, but where the code is assigned later by a coder (post-coding.) In the production of a concept descriptor, original text may thus exist without a code.
NOTE: Although post-coding is often performed from free text information, such as documents, scanned images or dictation, multi-media data is explicitly not permitted as original text. Also, the original text property is not meant to be a link into the entire source document. The link between different artifacts of medical information (e.g., document and coded result) is outside the scope of this specification and is maintained elsewhere in the HL7 standards. The original text is an excerpt of the relevant information in the original sources, rather than a pointer or exact reproduction. Thus the original text is to be represented in plain text form.
Values of type may have a non-NULL original text property despite having a NULL code. Any value with code of NULL signifies a coding exception. In this case, originalText is a name or description of the concept that was not coded. Such exceptional values may also contain translations. Such translations directly encode the concept described in originalText.
A can be demoted into an ST value representing only the originalText of the value.
|
2.11.7
Translation : SET<CD>, inherited from CD
Definition: A set of other concept descriptors that translate this concept descriptor into other code systems.
translation is a set of other s that each translate the first into different code systems. Each element of the translation set was translated from the first . Each translation may, however, also contain translations. Thus, when a code is translated multiple times the information about which code served as the input to which translation will be preserved.
NOTE: The translations are quasi-synonyms of one real-world concept. Every translation in the set is supposed to express the same meaning "in other words." However, exact synonymy rarely exists between two structurally different coding systems. For this reason, not all of the translations will be equally exact.
2.11.8
Qualifier : LIST<CR>, (fixed)
|
2.12
Character String with Code (SC) specializes ST
Definition: A character string that optionally may have a code attached. The text must always be present if a code is present. The code is often a local code.
|
SC is used in cases where coding is exceptional (e.g., user text messages are essentially text messages, and a printable message is the important content. Yet, sometimes messages come from a catalog of canned messages, which SC allows to reference.
Any non-null SC value MAY have a code, however, a code MUST NOT be given without the text.
|
2.12.1
Code : CE
Definition: A code representing the string data. For example, the string data may be a user-message out of a message-catalog where the code represents the identifier of the message in the message catalog.
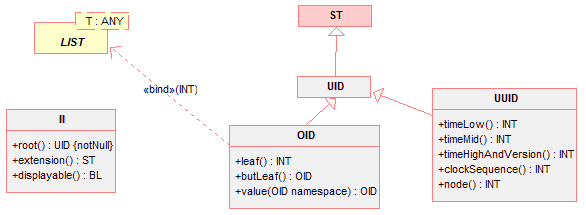
Instance Identifier data types.
2.13
Unique Identifier String (UID) specializes ST
Definition: A unique identifier string is a character string which identifies an object in a globally unique and timeless manner. The allowable formats and values and procedures of this data type are strictly controlled by HL7. At this time, user-assigned identifiers may be certain character representations of ISO Object Identifiers (OID) and DCE Universally Unique Identifiers (UUID). HL7 also reserves the right to assign other forms of UIDs (RUID), such as mnemonic identifiers for code systems.
The sole purpose of UID is to be a globally and timelessly unique identifier. The form of UID, whether it is an OID, a UUID or a RUID, is entirely irrelevant. As far as HL7 is concerned, the only thing one can do with a UID is denote to the object for which it stands. Comparison of UIDs is literal, i.e. if two UIDs are literally identical, they are assumed to denote to the same object. If two UIDs are not literally identical they may not denote to the same object.
|
No difference in semantics is recognized between the different allowed forms of the UID. The different forms are not distinguished by a component within or aside from the identifier string itself.
Even though this specification recognizes no semantic difference between the different forms of the unique identifier forms, there are differences of how these identifiers are built and managed, which is the sole reason to define subtypes to the UID for each of the variants.
2.14
ISO Object Identifier (OID) specializes UID
Definition: A globally unique string representing an ISO Object Identifier (OID) in a form that consists only of numbers and dots (e.g., "2.16.840.1.113883.3.1"). According to ISO, OIDs are paths in a tree structure, with the left-most number representing the root and the right-most number representing a leaf.
Each branch under the root corresponds to an assigning authority. Each of these assigning authorities may, in turn, designate its own set of assigning authorities that work under its auspices, and so on down the line. Eventually, one of these authorities assigns a unique (to it as an assigning authority) number that corresponds to a leaf node on the tree. The leaf may represent an assigning authority (in which case the root OID identifies the authority), or an instance of an object. An assigning authority owns a namespace, consisting of its sub-tree.
OIDs are the preferred scheme for unique identifiers. OIDs should always be used except if one of the inclusion criteria for other schemes apply.
ISO/IEC 8824:1990(E) clause 28 defines the Object Identifier as
28.9 The semantics of an object identifier value are defined by reference to an object identifier tree. An object identifier tree is a tree whose root corresponds to [the ISO/IEC 8824 standard] and whose vertices [i.e. nodes] correspond to administrative authorities responsible for allocating arcs [i.e. branches] from that vertex. Each arc from that tree is labeled by an object identifier component, which is [an integer number]. Each information object to be identified is allocated precisely one vertex (normally a leaf) and no other information object (of the same or a different type) is allocated to that same vertex. Thus an information object is uniquely and unambiguously identified by the sequence of [integer numbers] (object identifier components) labeling the arcs in a path from the root to the vertex allocated to the information object.
28.10 An object identifier value is semantically an ordered list of object identifier component values. Starting with the root of the object identifier tree, each object identifier component value identifies an arc in the object identifier tree. The last object identifier component value identifies an arc leading to a vertex to which an information object has been assigned. It is this information object, which is identified by the object identifier value. [...]
|
According to ISO/IEC 8824 an object identifier is a sequence of object identifier component values, which are integer numbers. These component values are ordered such that the root of the object identifier tree is the head of the list followed by all the arcs down to the leaf representing the information object identified by the OID. The fact that OID specializes LIST<INT> represents this path of object identifier component values from the root to the leaf.
The leaf and "butLeaf" properties take the opposite view. The leaf is the last object identifier component value in the list, and the "butLeaf" property is all of the OID but the leaf. In a sense, the leaf is the identifier value and all of the OID but the leaf refers to the namespace in which the leaf is unique and meaningful.
However, what part of the OID is considered value and what is namespace may be viewed differently. In general, any OID component sequence to the left can be considered the namespace in which the rest of the sequence to the right is defined as a meaningful and unique identifier value. The value-property with a namespace OID as its argument represents this point of view.31
|
2.14.1
HL7-Assigned OIDs
HL7 shall establish an OID registry and assign OIDs in its branch for HL7 users and vendors upon their request. HL7 shall also assign OIDs to public identifier-assigning authorities both U.S. nationally (e.g., the U.S. State driver license bureaus, U.S. Social Security Administration, HIPAA Provider ID registry, etc.) and internationally (e.g., other countries Social Security Administrations, Citizen ID registries, etc.) The HL7 registered OIDs must be used for these organizations, regardless whether these organizations have other OIDs assigned from other sources.
When assigning OIDs to third parties or entities, HL7 shall investigate whether an OID is already assigned for such entities through other sources. It this is the case, HL7 shall record such OID in a catalog, but HL7 shall not assign a duplicate OID in the HL7 branch. If possible, HL7 shall notify a third party when an OID is being assigned for that party in the HL7 branch.
Though HL7 shall exercise diligence before assigning an OID in the HL7 branch to third parties, given the lack of a global OID registry mechanism, one cannot make absolutely certain that there is no preexisting OID assignment for such third-party entity. Also, a duplicate assignment can happen in the future through another source. If such cases of supplicate assignment become known to HL7, HL7 shall make efforts to resolve this situation. For continued interoperability in the meantime, the HL7 assigned OID shall be the preferred OID used.
While most owners of an OID will "design" their namespace sub-tree in some meaningful way, there is no way to generally infer any meaning on the parts of an OID. HL7 does not standardize or require any namespace sub-structure. An OID owner, or anyone having knowledge about the logical structure of part of an OID, may still use that knowledge to infer information about the associated object; however, the techniques cannot be generalized.
An HL7 interface must not rely on any knowledge about the substructure of an OID for which it cannot control the assignment policies.
2.14.2
Literal Form
The structured definition of the OID is provided mostly to be faithful to the OID specification. Within HL7, OIDs are used as UID strings only, i.e., the literal string value is the only thing that is communicated and is the only thing that a reciever should have to consider when working with UIDs in the scope of the HL7 specification.
|
For compatibility with the DICOM standard, the literal form of the OID should not exceed 64 characters. (see DICOM part 5, section 9).
2.15
DCE Universal Unique Identifier (UUID) specializes UID
Definition: A globally unique string representing a DCE Universal Unique Identifier (UUID) in the common UUID format that consists of 5 hyphen-separated groups of hexadecimal digits having 8, 4, 4, 4, and 12 places respectively.
Both the UUID and its string representation are defined by the Open Group, CDE 1.1 Remote Procedure Call specification, Appendix A.
UUIDs are assigned based on Ethernet MAC addresses, the point in time of creation and some random component. This mix is believed to generate sufficiently unique identifiers without any organizational policy for identifier assignment (in fact this piggy-backs on the organization of MAC address assignment.)
UUIDs are not the preferred identifier scheme for use as HL7 UIDs. UUIDs may be used when identifiers are issued to objects representing individuals (e.g., entity instance identifiers, act event identifiers, etc.) For objects describing classes of things or events (e.g., catalog items), OIDs are the preferred identifier scheme.
|
2.15.1
Literal Form
The structured definition of the UUID is provided mostly to be faithful to the UUID specification. Within HL7, UUIDs are used as UID strings only, i.e., the literal string value is the only thing that is communicated and is the only thing that a reciever should have to consider when working with UIDs in the scope of the HL7 specification.
The literal form for the UUID is defined according to the original specification of the UUID. However, because the HL7 UIDs are case sensitive, for use with HL7, the hexadecimal digits A-F in UUIDs must be converted to upper case.
NOTE: The output of UUID related programs and functions may use all sorts of forms, upper case, lower case, and with or without the hyphens that group the digits. This variate output must be postprocessed to conform to the HL7 specification, i.e., the hyphens must be inserted for the 8-4-4-4-12 grouping and all hexadecimal digits must be converted to upper case.
2.16
HL7 Reserved Identifier Scheme (RUID) specializes UID
Definition: A globally unique string defined exclusively by HL7. Identifiers in this scheme are only defined by balloted HL7 specifications. Local communities or systems must never use such reserved identifiers based on bilateral negotiations.
HL7 reserved identifiers are strings that consist only of (US-ASCII) letters, digits and hyphens, where the first character must be a letter. HL7 may assign these reserved identifiers as mnemonic identifiers for major concepts of interest to HL7.
2.17
Instance Identifier (II) specializes ANY
Definition: An identifier that uniquely identifies a thing or object. Examples are object identifier for HL7 RIM objects, medical record number, order id, service catalog item id, Vehicle Identification Number (VIN), etc. Instance identifiers are defined based on ISO object identifiers.
|
2.17.1
Root : UID
Definition: A unique identifier that guarantees the global uniqueness of the instance identifier. The root alone may be the entire instance identifier.
In the presence of a non-null extension, the root is commonly interpreted as the "assigning authority", that is, it is supposed that the root somehow refers to an organization that assigns identifiers sent in the extension. However, the root does not have to be an organizational UID, it can also be a UID specifically registered for an identifier scheme.32
|
2.17.2
Extension : ST
Definition: A character string as a unique identifier within the scope of the identifier root.
The extension is a character string that is unique in the namespace designated by the root. If a non-NULL extension is exists, the root specifies a namespace (sometimes called "assigning authority" or "identifier type".) The extension property may be NULL in which case the root OID is the complete unique identifier.
The root and extension scheme effectively means that the concatenation of root and extension must be a globally unique identifier for the item that this II value identifies.
It is recommended that systems use the OID scheme for external identifiers of their communicated objects. The extension property is mainly provided to accommodate legacy alphanumeric identifier schemes.
Some identifier schemes define certain style options to their code values. For example, the U.S. Social Security Number (SSN) is normally written with dashes that group the digits into a pattern "123-12-1234". However, the dashes are not meaningful and a SSN can just as well be represented as "123121234" without the dashes.
In the case where identifier schemes provide for multiple representations, HL7 shall make a ruling about which is the preferred form. HL7 shall document that ruling where that respective external identifier scheme is recognized. HL7 shall decide upon the preferred form based on criteria of practicality and common use. In absence of clear criteria of practicality and common use, the safest, most extensible, and least stylized (the least decorated) form shall be given preference.33
HL7 may also decide to map common external identifiers to the value portion of the II.root OID. For example, the U.S. SSN could be represented as 2.16.840.1.113883.4.1.123121234. The criteria of practicality and common use will guide HL7's decision on each individual case.
2.17.3
Assigning Authority Name : ST
Definition: A human readable name or mnemonic for the assigning authority. The Assigning Authority Name has no computational value. The purpose of a Assigning Authority Name is to assist an unaided human interpreter of an II value to interpret the authority. Note: no automated processing must depend on the assigning authority name to be present in any form.
2.17.4
Displayable : BL
Definition: Specifies if the identifier is intended for human display and data entry (displayable = true) as opposed to pure machine interoperation (displayable = false).
2.17.5
Equality : BL, inherited from ANY
Two instance identifiers are equal if and only if their root and extension properties are equal.
|
URL And TEL data types
2.18
Universal Resource Locator (URL) specializes ANY
Definition: A telecommunications address specified according to Internet standard RFC 2396 [http://www.ietf.org/rfc/rfc2396.txt]. The URI specifies the protocol and the contact point defined by that protocol for the resource. Notable uses of the telecommunication address data type are for telephone and telefax numbers, e-mail addresses, Hypertext references, FTP references, etc.
The Internet standard RFC 2396 [http://www.ietf.org/rfc/rfc2396.txt] defines a URI as follows:
Just as there are many different methods of access to resources, there are several schemes for describing the location of such resources. The generic syntax for URLs provides a framework for new schemes to be established using protocols other than those defined in this document.
URLs are used to "locate" resources, by providing an abstract identification of the resource location. Having located a resource, a system may perform a variety of operations on the resource, as might be characterized by such words as "access", "update", "replace", "find attributes". In general, only the "access" method needs to be specified for any URL scheme.
By agreement, it is permissable to use a URI in place of a URL. In these cases, it is still expected that the resources identified is accessible by some agreed method. A common use of URI's is to refer to SOAP attachments
|
2.18.1
Scheme : CS
Definition: Identifies the protocol used to interpret the address string and to access the resource so addressed.
Some URL schemes are registered by the Internet Assigned Numbers Authority (IANA) [http://www.iana.org], however IANA only registers URL schemes that are defined in Internet RFC documents. In fact there are a number of URL schemes defined outside RFC documents, part of which are registered with the World Wide Web Consortium (W3C).34
Similar to the ED.mediaType, HL7 makes suggestions about scheme values classifying them as required, recommended, other, and deprecated. Any scheme not mentioned has status other.
Note that this specification explicitly limits itself to URLs. Universal Resource Names (URN) are not covered by this specification. URNs are a kind of identifier scheme for other than accessible resources. This specification, however, is only concerned with accessible resources, which belong into the URL category.
2.18.2
Address : ST
Definition: The address is a character string whose format is entirely defined by the scheme.
2.18.3
Literal Form
While conceptually URL has the properties scheme and address, the common appearance of a URL is as a string literal formed according to the Internet standard. The general syntax of the URL literal is:
|
Telephone and FAX Numbers
Note that there is no special data type for telephone numbers, telephone numbers are TELs and are specified as URLs.
The telephone number URL is defined in Internet RFC 2806 [http://www.ietf.org/rfc/rfc2806.txt]. Its definition is summarized in this subsection. This summary does not override or change any of the Internet specification's rulings.
The voice telephone URLs begin with "tel:" and fax URLs begin with "fax:"
The address is the telephone number in accordance with ITU-T E.123 Telephone Network and ISDN Operation, Numbering, Routing and Mobile Service: Notation for National and International Telephone Numbers (1993). While HL7 does not add or withdraw from the URL specification, the preferred subset of the address address syntax is given as follows:
|
The global absolute telephone numbers starting with the "+" and country code are preferred. Separator characters serve as decoration but have no bearing on the meaning of the telephone number. For example: "tel:+13176307960" and "tel:+1(317)630-7960" are both the same telephone number; "fax:+49308101724" and "fax:+49(30)8101-724" are both the same fax number.
2.19
Telecommunication Address (TEL) specializes URL
Definition: A telephone number (voice or fax), e-mail address, or other locator for a resource mediated by telecommunication equipment. The address is specified as a Universal Resource Locator (URL) qualified by time specification and use codes that help in deciding which address to use for a given time and purpose.
The semantics of a telecommunication address is that a communicating entity (the responder) listens and responds to that address, and therefore can be contacted by an other communicating entity (the initiator.)
The responder of a telecommunication address may be an automatic service that can respond with information (e.g., FTP or HTTP services.) In such case a telecommunication address is a reference to that information accessible through that address. A telecommunication address value can thus be resolved to some information (in the form of encapsulated data, ED.)
|
The telecommunication address is an extension of the Universal Resource Locator (URL) specified according to Internet standard RFC 2396 [http://www.ietf.org/rfc/rfc2396.txt]. The URL specifies the protocol and the contact point defined by that protocol for the resource. Notable use cases for the telecommunication address data type are for telephone and fax numbers, e-mail addresses, Hypertext references, FTP references, etc.
2.19.1
Useable Period : GTS
Definition: Specifies the periods of time during which the telecommunication address can be used. For a telephone number, this can indicate the time of day in which the party can be reached on that telephone. For a web address, it may specify a time range in which the web content is promised to be available under the given address.
2.19.2
Use Code : SET<CS>
Definition: One or more codes advising a system or user which telecommunication address in a set of like addresses to select for a given telecommunication need.
The telecommunication use code is not a complete classification for equipment types or locations. Its main purpose is to suggest or discourage the use of a particular telecommunication address. There are no easily defined rules that govern the selection of a telecommunication address.
2.19.3
Equality : BL, inherited from ANY
Two telecommunication address values are considered equal if both their URLs are equal. Use code and valid time are excluded from the equality test.
|
2.20
Address Part (ADXP) specializes ST
Definition: A character string that may have a type-tag signifying its role in the address. Typical parts that exist in about every address are street, house number, or post box, postal code, city, country but other roles may be defined regionally, nationally, or on an enterprise level (e.g. in military addresses). Addresses are usually broken up into lines, which are indicated by special line-breaking delimiter elements (e.g., DEL).
|
2.20.1
Address Part Type : CS
Definition: Specifies whether an address part names the street, city, country, postal code, post box, etc. If the type is NULL the address part is unclassified and would simply appear on an address label as is.
2.21
Postal Address (AD) specializes LIST<ADXP>
Definition: Mailing and home or office addresses. A sequence of address parts, such as street or post office Box, city, postal code, country, etc.
AD is primarily used to communicate data that will allow printing mail labels, that will allow a person to physically visit that address. The postal address data type is not supposed to be a container for additional information that might be useful for finding geographic locations (e.g., GPS coordinates) or for performing epidemiological studies. Such additional information is captured by other, more appropriate HL7 elements.
Addresses are conceptualized as text with added logical mark-up. The mark-up may break the address into lines and may describe in detail the role of each address part if it is known. Address parts occur in the address in the order in which they would be printed on a mailing label. The approach is similar to HTML or XML markup of text (but it is not technically limited to XML representations.)
Addresses are essentially sequences of address parts, but add a "use" code and a valid time range for information about if and when the address can be used for a given purpose.
|
2.21.1
Use Code : SET<CS>
Definition: A set of codes advising a system or user which address in a set of like addresses to select for a given purpose.
An address without specific use code might be a default address useful for any purpose, but an address with a specific use code would be preferred for that respective purpose.
2.21.2
Useable Period : GTS
Definition: A General Timing Specification (GTS) specifying the periods of time during which the address can be used. This is used to specify different addresses for different times of the week or year.
2.21.3
Is Not Ordered : BL
Definition: A boolean value specifying whether the order of the address parts is known or not. While the address parts are always a Sequence, the order in which they are presented may or may not be known. Where this matters, the isNotOrdered property can be used to convey this information.
2.21.4
Equality : BL, inherited from ANY
Two address values are considered equal if both contain the same address parts, independent of ordering. Use code and valid time are excluded from the equality test.
|
2.21.5
Formatting Address : ST
Definition: A character string value with the address formatted in lines and with proper spacing. This is only a semantic property to define the function of some of the address part types.36
The AD data type's main purpose is to capture postal addresses, such that one can visit that address or send mail to it. Humans will look at addresses in printed form, such as on a mailing label. The AD data type defines precise rules of how its data is formatted.37
Addresses are ordered lists of address parts. Each address part is printed in the order of the list from left to right and top to bottom (or in any other language-specific reading direction, which to determine is outside the scope of this specification.) Every address part value is printed. Most address parts are framed by white space. The following six rules govern the setting of whitespace.
- Whitespace never accumulates, i.e. two subsequent spaces are the same as one. Subsequent line breaks can be reduced to one. Whitespace around a line break is not significant.
- Literals may contain explicit whitespace, subject to the same white space reduction rules. There is no notion of a literal line break within the text of a single address part.
- Leading and trailing explicit whitespace is insignificant in all address parts, except for delimiter (DEL) address parts.
- By default, an address part is surrounded by implicit whitespace.
- Delimiter (DEL) address parts are not surrounded by any implicit white space.
- Leading and trailing explicit whitespace is significant in delimiter (DEL) address parts.
This means that all address parts are generally surrounded by white space, but whitespace does never accumulate. Delimiters are never surrounded by implicit whitespace and every whitespace contributed by preceding or succeeding address parts is discarded, whether it was implicit or explicit.
The following shows examples of addresses in the XML ITS form.
1050 W Wishard Blvd,
RG 5th floor,
Indianapolis, IN 46240.
Can be encoded in any of the following forms:38
The first form would result from a system that only stores addresses as free text or in a list of fields line1, line2, etc.:
<addr use="WP"> 1050 W Wishard Blvd, RG 5th floor, Indianapolis, IN 46240 </addr> |
The second form is more specific about the role of the address parts than the first one:
<addr use="WP"> <streetAddressLine>1050 W Wishard Blvd</streetAddressLine>, <streetAddressLine>RG 5th floor</streetAddressLine>, <city>Indianapolis</city>, <state>IN</state> <postalCode>46240</postalCode> </addr> |
This form is the typical form seen in the U.S., where street address is sometimes separated, and city, state and ZIP code are always separated.
The third is even more specific:
<addr use="WP"> <houseNumber>1050</houseNumber> <direction>W</direction> <streetName>Wishard Blvd</streetName>, <additionalLocator>RG 5th floor</additionalLocator>, <city>Indianapolis</city>, <state>IN</state> <postalCode>46240</postalCode> </addr> |
The latter form above is not used in the USA. However, it is useful in Germany, where many systems keep house number as a distinct field. For example, the German address:
Windsteiner Weg 54a,
D-14165 Berlin
would most likely be encoded as follows39
<addr use="HP"> <streetName>Windsteiner Weg</streetName> <houseNumber>54a</houseNumber>, <country>D</country>- <postalCode>14165</postalCode> <city>Berlin</city> </addr> |
2.22
Entity Name Part (ENXP) specializes ST
Definition: A character string token representing a part of a name. May have a type code signifying the role of the part in the whole entity name, and a qualifier code for more detail about the name part type. Typical name parts for person names are given names, and family names, titles, etc.
|
2.22.1
Name Part Type : CS
Definition: Indicates whether the name part is a given name, family name, prefix, suffix, etc.
Not every name part must have a type code, if the type code is unknown, not applicable, or simply undefined this is expressed by a NULL value (type.isNull). For example, a name may be "Rogan Sulma" and it may not be clear which one is a given name or which is a last name, or whether Rogan may be a title.
Entity names are conceptualized as text with added mark-up. The mark-up may describe in detail the role of each name part if it is known. Name parts occur in the order in which they would be printed on a mailing label. The model is similar to HTML or XML markup of text.
2.22.2
Qualifier : SET<CS>
Definition: The qualifier is a set of codes each of which specifies a certain subcategory of the name part in addition to the main name part type. For example, a given name may be flagged as a nickname, a family name may be a pseudonym or a name of public records.
2.23
Entity Name (EN) specializes LIST<ENXP>
Definition: A name for a person, organization, place or thing. A sequence of name parts, such as given name or family name, prefix, suffix, etc. Examples for entity name values are "Jim Bob Walton, Jr.", "Health Level Seven, Inc.", "Lake Tahoe", etc. An entity name may be as simple as a character string or may consist of several entity name parts, such as, "Jim", "Bob", "Walton", and "Jr.", "Health Level Seven" and "Inc.", "Lake" and "Tahoe".
Entity names are conceptualized as text with added logical mark-up. Name parts occur in a natural order in which they would be displayed, as opposed to in a order detemined by name part. The ordeing of the name parts is significant a feature that replaces the need for a separate "display name" property. Applications may change that ordering of name parts to account for their user's customary ordering of name parts. The approach is similar to HTML or XML markup of text (but it is not technically limited to XML representations.)
Entity names are essentially sequences of entity name parts, but add a "use" code and a valid time range for information about when the name was used and how to choose between multiple aliases that may be valid at the same point in time.
|
2.23.1
Use Code : SET<CS>
Definition: A set of codes advising a system or user which name in a set of names to select for a given purpose.
A name without specific use code might be a default name useful for any purpose, but a name with a specific use code would be preferred for that respective purpose.
2.23.2
Valid Time : IVL<TS>
Definition: An interval of time specifying the time during which the name is or was used for the entity. This accomodates the fact that people change names for people, places and things.
EN conforms to the history item data type extension (HXIT).
2.23.3
Equality : BL, inherited from ANY
Two name values are considered equal if both conatain the same name parts, independent of ordering. Use code and valid time are excluded from the equality test.
|
2.23.4
Formatting Entity Names : ST
Definition: A character string value with the entity name formatted with proper spacing. This is only a semantic property to define the function of some of the name part types.41
The EN data type's main purpose is to capture names of people, places, and things (entities), so that one can address and refer to these entities in speech and writing. Humans will look at names in printed form, such as on a mailing label. The EN data type therefore defines precise rules of how its data is formatted.42
Entity names are ordered lists of entity name parts. Each entity name part is printed in the order of the list from left to right (or in any other language-specific reading direction.) Every entity name part (except for those marked "invisible") is printed. Most entity name parts are framed by whitespace. The following six rules govern the setting of whitespace.
- Whitespace never accumulates, i.e. two subsequent spaces are the same as one.
- Literals may contain explicit whitespace subject to the same white space reduction rules.
- Except for prefix, suffix and delimiter name parts, every name part is surrounded by implicit whitespace. Leading and trailing explicit whitespace is insignificant in all those name parts.
- Delimiter name parts are not surrounded by any implicit white space. Leading and trailing explicit whitespace is significant in delimiter name parts.
- Prefix name parts only have implicit leading whitespace but no implicit trailing whitespace. Trailing explicit whitespace is significant in prefix name parts.
- Suffix name parts only have implicit trailing whitespace but no implicit leading whitespace. Leading explicit whitespace is significant in suffix name parts.
- This means that all entity name parts are generally surrounded by whitespace, but whitespace does never accumulate. Delimiters are never surrounded by implicit whitespace, prefixes are not followed by implicit whitespace and suffixes are not preceded by implicit white space. Every whitespace contributed by preceding or succeeding name parts around those special name parts is discarded, whether it was implicit or explicit.
2.23.5
Examples
A very simple encoding of "Adam A. Everyman" would be:
<name> <given>Adam</given> <given>A.</given> <family>Everyman</family> </name> |
None of the special qualifiers need to be mentioned if they are unknown or irrelevant. The next example shows extensive use of multiple given names, prefixes, suffixes, for academic degrees, nobility titles, vorvoegsels ("van"), and professional designations.
<name> <prefix qualifier="AC">Dr. phil. </prefix> <given>Regina</given> <given>Johanna</given> <given>Maria</given> <prefix qualifier="NB">Gräfin </prefix> <family qualifier="BR">Hochheim</family>-<family qualifier="SP">Weilenfels</family> <suffix qualifier="PR">NCFSA</suffix> </name> |
The next example is an organization name, "Health Level Seven, Inc." in simple string form:
<name>Health Level Seven, Inc.</name> |
and as a fully parsed name
<name>Health Level Seven, <suffix qualifier="LS">Inc.</suffix></name> |
The following example shows a Japanese name in the three forms: ideographic (Kanji), syllabic (Hiragana), and alphabetic (Romaji).
<name use="IDE"> <family>木村</family> <given>通男</given> </name> <name use="SYL"> <family>きむら</family> <given>みちお</given> </name> <name use="ABC"> <family>KIMURA</family> <given>MICHIO</given> </name> |
2.24
Trivial Name (TN) specializes EN
Definition: A restriction of entity name that is effectively a simple string used for a simple name for things and places.
TN is an EN that consists of only one name part without any name part type or qualifier. The TN, and its single name part are therefore equivalent to a simple character string. This equivalence is expressed by a defined demotion to ST and promotion from ST.
Trivial names are typically used for places and things, such as Lake Erie or Washington-Reagan National Airport:
<name>Lake Erie</name> <name>Washington-Reagan National Airport</name> |
2.25
Person Name (PN) specializes EN
Definition: An EN used when the named Entity is a Person. A sequence of name parts, such as given name or family name, prefix, suffix, etc. A name part is a restriction of entity name part that only allows those entity name parts qualifiers applicable to person names. Since the structure of entity name is mostly determined by the requirements of person name, the restriction is very minor.
Since most of the functionality of entity name is in support of person names, the person name (PN) is only a very minor restriction on the entity name part qualifier.
|
2.26
Organization Name (ON) specializes EN
Definition: An EN used when the named Entity is an Organization. A sequence of name parts.
A name for an organization, such as "Health Level Seven, Inc." An organization name consists only of untyped name parts, prefixes, suffixes, and delimiters.
|
2.26.1
Examples
The following is the organization name, "Health Level Seven, Inc." in a simple string form:
<name>Health Level Seven, Inc.</name> |
And with the legal status "Inc." as a distinguished name part:
<name>Health Level Seven, <suffix qualifier="LS">Inc.</suffix></name> |
2.27
Abstract Type Quantity (QTY) specializes ANY
Definition: The quantity data type is an abstract generalization for all data types (1) whose value set has an order relation (less-or-equal) and (2) where difference is defined in all of the data type's totally ordered value subsets. The quantity type abstraction is needed in defining certain other types, such as the interval and the probability distribution.
2.27.1
Ordering: less-or-equal : BL
Definition: A predicate expressing an order relation that is reflexive, asymmetric and transitive, between this quantity and another quantity.
The lessOrEqual relation is defined on any totally ordered partition of the quantity data type. A totally ordered partition is a subset of the data types's defined values where all elements have a defined order (e.g., the integer and real numbers are totally ordered.)
By contrast, a partially ordered set is a set where some, but not all pairs of elements are comparable through the order relation (e.g., a tree structure or the set of physical quantities is a partially ordered set.) Two data values x and y of an ordered type are comparable (x.compares(y)) if the less-or-equal relation holds in either way (x ≤ y or y ≤ x).
A partial order relation generates totally ordered subsets whose union is the entire set (e.g., the set of all length is a totally ordered subset of the set of all physical quantities.)
For example, a tree structure is partially ordered, where the root is considered less or equal to a leaf, but there may not be an order among the leafs. Also, physical quantities are partially ordered, since an order exists only among quantities of the same dimension (e.g., between two lengths, but not between a length and a time.) A totally ordered subset of a tree is a path that transitively connects a leaf to the root. The physical dimension of time is a totally ordered subset of physical quantities.
|
2.27.2
Equality : BL, inherited from ANY
Definition: Equality is a reflexive, symmetric, and transitive relation between any two data values. Only proper values can be equal, null values never are equal (even if they have the same null flavor.)
|
How equality is determined must be defined for each data type. If nothing else is specified, two data values are equal if they are indistinguishable, that is, if they differ in none of their semantic properties. A data type can "override" this general definition of equality, by specifying its own equal relationship. This overriding of the equality relation can be used to exclude semantic properties from the equality test. If a data type excludes semantic properties from its definition of equality, this implies that certain properties (or aspects of properties) that are not part of the equality test are not essential to the meaning of the value.
For example the physical quantity has the two semantic properties (1) a real number and (2) a coded unit of measure. The equality test, however, must account for the fact that, e.g., 1 meter equals 100 centimeters; independent equality of the two semantic properties is too strong a criterion for the equality test. Therefore, physical quantity must override the equality definition.
2.27.3
Comparability : BL
Definition: A predicate indicating if this value and the operand can be compared as to which is greater than the other.
Two quantities are comparable if they are both elements of a common totally ordered partition of their data types' value space. The definition is based on lessOrEqual.
|
2.27.4
DifferenceDataType : TYPE
Definition: The type of the difference between 2 values of a specific QTY data type.
|
The type will be some data type that further specializes QTY
2.27.5
Difference : QTY
Definition: A quantity expressing the "distance" of this quantity from the operand quantity, that must be comparable. The data type of the difference quantity is related to the operand quantities but need not be the same.
|
The result of minus has the data type returned by the diffType property of the instance.
A difference is defined in an ordered set if it is semantically meaningful to state that Δ is the difference between the values x and y. This difference Δ must be meaningful independently from the values x and y. This independence exists if for all values u one can meaningfully derive a value v such that Δ would also be the difference between u and v. The judgment for what is meaningful cannot be defined formally.43
minus has a data type that can express the difference between two values for which the ordering relation is defined (i.e., two elements of a common totally ordered subset.) For example, the difference data type of integer number is integer number, but the difference type of point in time is a physical quantity in the dimension of time. A difference data type is a totally ordered data type.
The difference between two values x minus y must be defined for all x and y in a common totally ordered subset of the data type's value set. Zero is the difference between a value and itself.
|
If x and y are not comparable, then the difference will be Null
|
2.27.6
Addition : QTY
Definition: The sum of this quantity and its operand. The operand must be of a data type that can express the difference between two values of this quantity's data type.
|
Q: what is the relationship between {y.dataType.implies(x.diffType)} and {x.compares(y)}?
If y is not a valid type for the difference between two values of the type of x, the the result of the operation will be NULL.
|
2.27.7
The Zero-Quantity : BL
Definition: The neutral element in the difference and addition operations, i.e., if a quantity is zero, addition to, or subtraction from any other comparable quantity will result in that other quantity.
|
2.27.8
Ordering: less-than : BL
Definition: A predicate expressing an order relation that is asymmetric and transitive, between this quantity and another quantity. The ordering is the same as lessOrEqual, but irreflexive.
|
2.27.9
Ordering: greater-or-equal : BL
Definition: A predicate expressing an order relation that is reflexive, asymmetric and transitive, between this quantity and another quantity. This is the inverse order of lessOrEqual.
|
2.27.10
Ordering: greater-than : BL
Definition: A predicate expressing an order relation that is asymmetric and transitive, between this quantity and another quantity. This is the invese of lessThan.
|
2.28
Integer Number (INT) specializes QTY
Definition: Integer numbers (-1,0,1,2, 100, 3398129, etc.) are precise numbers that are results of counting and enumerating. Integer numbers are discrete, the set of integers is infinite but countable. No arbitrary limit is imposed on the range of integer numbers. Two NULL flavors are defined for the positive and negative infinity.
Since the integer number data type includes all of the semantics of the mathematical integer number concept, the basic operations plus (addition) and times (multiplication) are defined. These operations are defined here as characterizing operations in the sense of ISO 11404, and because these operations are needed in other parts of this specification, namely the semantics of the literal form.
The traditional recursive definitions of addition and multiplication are due to Grassmann, and use the notion of successor.44
|
2.28.1
Successor : INT
Definition: The INT value that is greater than this INT value but where no INT value exists between this value and its successor.
|
2.28.2
DifferenceDataType : TYPE, inherited from QTY
|
The difference between two INT values is also a INT value.
2.28.3
Addition : INT, inherited from QTY
|
2.28.4
Multiplication : INT
Definition: The result of multiplying this integer with the operand, equivalent to repeated additions of this integer.
|
2.28.5
Predecessor : INT
Definition: The inverse of successor.
|
2.28.6
Negation : INT
Definition: The inverse element of the INT value, another INT value, which, when added to that value yields zero (the neutral element.)
|
2.28.7
Non-Negative : BL
Definition: A predicate indicating whether the INT zero (neutral element) is less or equal to this INT.
|
2.28.8
Negative : BL
Definition: A predicate indicating whether this INT is less than zero (not non-negative.)
|
2.28.9
Integer Division : INT
Definition: The integer division operation of this integer (dividend) with another integer (divisor) is the integer number of times the divisor fits into the dividend.
|
2.28.10
Remainder : INT
Definition: The remainder of the integer division.
|
This definition of the remainder matches the C and Java programming languages.
2.28.11
Neutral Element of Multiplication : BL
Definition: A predicate indicating if this value is the number one, i.e., the neutral element of multiplication. There is exactly one integer that has this property.
|
2.28.12
Literal Form
The literal form of an integer is a simple decimal number, i.e. a string of decimal digits.
|
2.29
Real Number (REAL) specializes QTY
Definition: Fractional numbers. Typically used whenever quantities are measured, estimated, or computed from other real numbers. The typical representation is decimal, where the number of significant decimal digits is known as the precision.
The term "Real number" in this specification is used to mean that fractional values are covered without necessarily implying the full set of the mathematical real numbers that would include irrational numbers such as ρ, Euler's number, etc.45
NOTE: This specification defines the real number data type in the broadest sense possible. However, it does not imply that any conforming ITS or implementation must be able to represent the full range of Real numbers, which would not be possible in any finite implementation. HL7's current use cases for the Real number data type are measured and estimated quantities and monetary amounts. These use cases can be handled with a restricted Real value space, rational numbers, and even just very limited decimals (scaled integers.) However, we declare the representations of the real value space as floating point, rational, scaled integer, or digit string, and their various limitations to be out of the scope of this specification.
This specification offers two choices for a number data type. The choice is made as follows: Any number attribute is a real if it is not known for sure that it is an integer. A number is an integer if it is always counted, typically representing an ordinal number. If there are conceivable use cases where such a number would be estimated or averaged, it is not always an integer and thus should use the Real data type.
The algebraic operations are specified here as characterizing operations in the sense of ISO 11404, and because these operations are needed in other parts of this specification.
Unlike the integer numbers, the real numbers semantics are not inductively constructed but only intuitively described by their axioms of their algebraic properties. The completeness axioms are intentionally left out so as to make no statement about irrational numbers.
2.29.1
Comparability : BL, inherited from QTY
The value set of REAL is totally ordered.
|
2.29.2
DifferenceDataType : TYPE, inherited from QTY
|
The difference between two REAL values is also a REAL value.
2.29.3
Addition : QTY, inherited from QTY
|
2.29.4
Negation (Inverse Element of Addition) : REAL
Definition: A REAL value, which, when added to another REAL value yields zero (the neutral element of addition.)
|
2.29.5
Neutral Element of Multiplication : BL
Definition: A predicate indicating if this value is the number one, i.e., the neutral element of multiplication. There is exactly one real number that has this property.
|
2.29.6
Multiplication : REAL
Definition: An operation in REAL that forms an abelian group and is related to addition by the law of distribution.
|
2.29.7
Inverse Element of Multiplication : REAL
Definition: A REAL value, which, when muliplied with another REAL value yields one (the neutral element of multiplication). Zero (the neutral element of addition) has no inverse element.
|
2.29.8
Homomorphism of INT into REAL : INT
The INT and REAL data types are related by a homomorphism that maps every value in INT to a value in REAL whereby the algebraic properties of INT are preserved. This means, an integer can be promoted to a real and a real can be demoted to an integer by means of rounding off the fractional part.
|
2.29.9
Exponentiation : REAL
Definition: The basis of exponentiation is the iterative multiplication of a real number, and extended to rational exponents as the inverse operation.
We only list certain common properties of exponentiation.
|
2.29.10
Literal Form
The literal form of an real is a string of decimal digits with optional leading "+" or "-" sign, and optional decimal point, and optional exponential notation using a case insensitive "e" between the mantissa and the exponent. The number of significant digits must conform to the precision property.
|
Examples of real literals for two thousand are 2000, 2000., 2e3, 2.0e+3, +2.0e+3.
Note that the literal form does not carry type information. For example, "2000" is a valid representation of both a real number and an integer number. No trailing decimal point is used to disambiguate from integer numbers. An ITS that uses this literal form must recover the type information from other sources.
2.29.11
Precision of the Decimal Form : INT
Definition: The number of significant digits of the decimal representation.
Precision is formally defined based on the literal
The precision attribute is only the precision of a decimal digit representation, not the accuracy of the real number value.
The purpose of the precision property for the real number data type is to faithfully capture the whole information presented to humans in a number. The amount of decimal digits shown conveys information about the uncertainty (i.e., precision and accuracy) of a measured value.
NOTE: The precision of the representation is independent from uncertainty (precision accuracy) of a measurement result. If the uncertainty of a measurement result is important, one should specify uncertain values as PPD.
The rules for what digits are significant are as follows:
- All non-zero digits are significant.
- All zeroes to the right of a significant digit are significant.
- When all digits in the number are zero the zero-digit immediately left to the decimal point is significant (and because of rule 2, all following zeroes are thus significant too.)
NOTE: These rules of significance differ slightly from the more casual rules taught in school. Notably trailing zeroes before the decimal point are consistently regarded significant here. Elsewhere, e.g., 2000 is ambiguous as to whether the zeroes are significant. This deviation from the common custom is warranted for the purpose of unambiguous communication.
The precision of the representation should match the uncertainty of the value. However, precision of the representation and uncertainty of the value are separate independent concepts. Refer to PPD<REAL> for details about uncertain real numbers.
For example "0.123" has 3 significant digits in the representation, but the uncertainty of the value may be in any digit shown or not shown, i.e., the uncertainty may be 0.123±0.0005, 0.123±0.005 or 0.123±0.00005, etc. Note that ITS representations should adjust their representational precision with the uncertainty of the value. However, since the precision in the digit string is granular to 0.5 the least significant digit, while uncertainty may be anywhere between these "grid lines", 0.123±0.005 would also be an adequate representation for the value between 0.118 and 0.128.
NOTE: On a character based Implementation Technology the ITS need not represent the precision as an explicit attribute if numbers are represented as decimal digit strings. In that case, the ITS must abide by the rules of an unambiguous determination of significant digits. A number representation must not produce more or less significant digits than were originally in that number. Conformance can be tested through round-trip encoding — decoding — encoding.
2.30
Ratio (RTO) specializes QTY
Definition: A quantity constructed as the quotient of a numerator quantity divided by a denominator quantity. Common factors in the numerator and denominator are not automatically cancelled out. The RTO data type supports titers (e.g., "1:128") and other quantities produced by laboratories that truly represent ratios. Ratios are not simply "structured numerics", particularly blood pressure measurements (e.g. "120/60") are not ratios. In many cases the REAL should be used instead of the RTO.
Ratios are different from rational numbers, i.e., in ratios common factors in the numerator and denominator never cancel out. A ratio of two real or integer numbers is not automatically reduced to a real number.
NOTE: This data type is not defined to generally represent rational numbers. It is used only if common factors in numerator and denominator are not supposed to cancel out. This is only rarely the case. For observation values, ratios occur almost exclusively with titers.
|
The default value for both numerator and denominator is the integer number 1 (one.) The denominator may not be zero.
NOTE: This data type is defined as a generic data type (see Generic Data Types (§ 1.9.5 )) but discussed in the context of the other quantity-related data types. The reason for defining RTO as a generic data type is so that it can be constrained precisely as to what the numerator and denominator types should be.
2.30.1
Numerator : N
Definition: The quantity that is being divided in the ratio. The default is the integer number 1 (one.)
2.30.2
Denominator : D
Definition: The quantity that devides the numerator in the ratio. The default is the integer number 1 (one.) The denominator must not be zero.
|
2.30.3
Literal Form
A ratio literal form exists for all ratios where both numerator and denominators have literal forms. A ratio is simply the numerator literal a colon as separator followed by the denominator literal. When the colon and denominator are missing, the integer number 1 is assumed as the denominator.
|
For example, the rubella virus antibody titer value 1:64 could be represented using the literal "1:64".
2.31
Physical Quantity (PQ) specializes QTY
Definition: A dimensioned quantity expressing the result of measuring.
| Name | Type | Description |
|---|---|---|
| value | REAL | The magnitude of the quantity measured in terms of the unit. |
| unit | CS | The unit of measure specified in the Unified Code for Units of Measure (UCUM) [http://aurora.rg.iupui.edu/UCUM]. |
| translation | SET<PQR> | An alternative representation of the same physical quantity expressed in a different unit, of a different unit code system and possibly with a different value. |
| canonical | PQ | A physical quantity expressed in a canonical unit. In any given unit system has every physical dimension can be assigned one canonical unit Defining the canonical unit is not subject of this specification, only asserting that such a canonical unit exists (and can be arbitrarily chosen) for every physical quantity. An abstract physical quantity is equal to its canonical form. |
| diffType | TYPE | The type of the difference between 2 values of a specific QTY data type. |
| toPQ | REAL |
2.31.1
Maginitude Value : REAL
Definition: The magnitude of the quantity measured in terms of the unit.
2.31.2
Unit of Measure : CS
Definition: The unit of measure specified in the Unified Code for Units of Measure (UCUM) [http://aurora.rg.iupui.edu/UCUM].
NOTE: Equality of physical quantities does not require the values and units to be equal independently. Value and unit is only how we represent physical quantities. For example, 1 m equals 100 cm. Although the units are different and the values are different, the physical quantities are equal! Therefore one should never expect a particular unit for a physical quantity but instead provide automated conversion between different comparable units.
2.31.3
Translation : SET<PQR>
Definition: An alternative representation of the same physical quantity expressed in a different unit, of a different unit code system and possibly with a different value.
Physical quantities semantically are the results of measurement acts. Although physical quantities are represented as pairs of value and unit, semantically, a physical quantity is more than that. To find out whether two physical quantities are equal, it is not enough to compare equality of their two values and units independently. For example, 100 cm equals 1 m although neither values nor units are equal. To define equality we introduce the notion of a canonical form.
2.31.4
Canonical Form : PQ
Definition: A physical quantity expressed in a canonical unit. In any given unit system has every physical dimension can be assigned one canonical unit Defining the canonical unit is not subject of this specification, only asserting that such a canonical unit exists (and can be arbitrarily chosen) for every physical quantity. An abstract physical quantity is equal to its canonical form.
|
For example, for a unit system based on the Système International (SI) one can define the canonical form as (a) the product of only the base units; (b) without prefixes; where (c) only multiplication and exponents are used (no division operation); and (d) where the seven base units appear in a defined ordering (e.g., m, s, g...) Thus, 1 mm Hg would be expressed as 133322 m-1 s-2. As can be seen, the rules how to build the canonical form of units may be quite complex. However, for the semantic specification it doesn't matter how the canonical form is built, nor what specific canonical form is chosen, only that some canonical form could be defined.
2.31.5
Equality : BL, inherited from ANY
Two physical quantities are equal if each their values and their units of their canonical forms are equal.
|
2.31.6
Comparability : BL, inherited from QTY
Two physical quantities compare each other (and have an ordering and difference) if the units of their canonical forms are equal.
|
2.31.7
DifferenceDataType : TYPE, inherited from QTY
|
The difference between 2 Physical Quantities is another Physical Quantity with the same units
|
2.31.8
Neutral Element of Multiplication : BL
Definition: A predicate indicating if this value is the number one, i.e., the neutral element of multiplication. There is exactly one physical quantity that has this property and is called the unity.
|
2.31.9
Multiplication : PQ
Definition: The product of two physical quantities is the product of their values times the product of their units.
|
2.31.10
Inverse Element of Multiplication : PQ
Definition: A PQ value, which, when muliplied with another PQ value yields one (the neutral element of multiplication). Zero (the neutral element of addition) has no inverse element. The quotient of two comparable quantities is comparable to the unity (the unit 1).
|
2.31.11
Real Multiplication : PQ
Definition: Multiplication with a real number forms a scaled quantity. A scaled quantity is comparable to its original quantity.
If two quantities Q1 and Q2 compare each other, there exists a real number r such that r1 = Q1 / Q2.
|
2.31.12
Homomorphism of REAL into PQ : REAL
A REAL value can be converted to a PQ value with the unity, i.e. the unit 1 (one). Likewise, a physical quantity that compares the unity can be converted to a real number.
|
2.31.13
Exponentiation : PQ
Definition: A physical quantity can be raised to an integer power.
|
2.31.14
Addition : PQ
Definition: Two physical quantities that compare each other can be added.
|
2.31.15
Literal Form
The literal form for a physical quantity is a real number literal followed by optional whitespace and a character string representing a valid code in the Unified Code for Units of Measure (UCUM) [http://aurora.rg.iupui.edu/UCUM].
|
For example, 20 minutes is "20 min".
2.32
Physical Quantity Representation (PQR) specializes CV
Definition: An extension of the coded value data type representating a physical quantity using a unit from any code system. Used to show alternative representation for a physical quantity.
|
2.32.1
Value : REAL
Definition: The magnitude of the measurement value in terms of the unit specified by this code.
2.32.2
Code : ST, inherited from CV
Definition: The plain code symbol defined by the code system. For example, "784.0" is the code symbol of the ICD-9 code "784.0" for headache.
A non-exceptional value has a non-NULL code property whose value is a character string that is a symbol defined by the coding system identified by codeSystem. Conversely, a value without a value for the code property, or with a value that is not from the cited coding system is an exceptional value (NULL of flavor other).
|
Definition: The plain code symbol defined by the code system. For example, "784.0" is the code symbol of the ICD-9 code "784.0" for headache.
A non-exceptional value has a non-NULL code property whose value is a character string that is a symbol defined by the coding system identified by codeSystem. Conversely, a value without a value for the code property, or with a value that is not from the cited coding system is an exceptional value (NULL of flavor other).
|
2.32.3
Code System : UID, inherited from CV
Definition: Specifies the code system that defines the code.
Code systems shall be referred to by a UID, which allows unambiguous reference to standard HL7 codes, other standard code systems, as well as local codes. HL7 shall assign a UID to each of its code tables as well as to external standard coding systems that are being used with HL7. Local sites must use their ISO Object Identifier (OID) to construct a globally unique local coding system identifier.
Under HL7's branch, 2.16.840.1.113883, the sub-branches 5 and 6 contain HL7 standard and external code system identifiers respectively. The HL7 Vocabulary Technical Committee maintains these two branches.
A non-exceptional value (i.e. a value that has a non-null code property) has a non-NULL codeSystem specifying the system of concepts that defines the code. In other words whenever there is a code there is also a code system.
NOTE: Although every non-NULL value has a defined code system, in some circumstances, the ITS representation for the value needs not explicitly mention the code system. For example, when the context mandates one and only one code system to be used specifying the code system explicitly would be redundant. However, in that case the codeSystem takes on that context-specific default value and is not NULL.
|
An exceptional of NULL-flavor other indicates that a concept could not be coded in the coding system specified. Thus, for these coding exceptions, the code system that did not contain the appropriate concept must be provided in codeSystem.
Some code domains are qualified such that they include the portion of any pertinent local coding system that does not simply paraphrase the standard coding system (coded with extensibility, CWE.) If a CWE qualified field actually contains such a local code, the coding system must specify the local coding system from which the local code was taken. However, for CWE domains the local code is a valid member of the domain, so that local codes in CWE domains constitute neither an error nor an exceptional (NULL/other) value in the sense of this specification.
|
Definition: Specifies the code system that defines the code.
Code systems shall be referred to by a UID, which allows unambiguous reference to standard HL7 codes, other standard code systems, as well as local codes. HL7 shall assign a UID to each of its code tables as well as to external standard coding systems that are being used with HL7. Local sites must use their ISO Object Identifier (OID) to construct a globally unique local coding system identifier.
Under HL7's branch, 2.16.840.1.113883, the sub-branches 5 and 6 contain HL7 standard and external code system identifiers respectively. The HL7 Vocabulary Technical Committee maintains these two branches.
A non-exceptional value (i.e. a value that has a non-null code property) has a non-NULL codeSystem specifying the system of concepts that defines the code. In other words whenever there is a code there is also a code system.
NOTE: Although every non-NULL value has a defined code system, in some circumstances, the ITS representation for the value needs not explicitly mention the code system. For example, when the context mandates one and only one code system to be used specifying the code system explicitly would be redundant. However, in that case the codeSystem takes on that context-specific default value and is not NULL.
|
An exceptional of NULL-flavor other indicates that a concept could not be coded in the coding system specified. Thus, for these coding exceptions, the code system that did not contain the appropriate concept must be provided in codeSystem.
Some code domains are qualified such that they include the portion of any pertinent local coding system that does not simply paraphrase the standard coding system (coded with extensibility, CWE.) If a CWE qualified field actually contains such a local code, the coding system must specify the local coding system from which the local code was taken. However, for CWE domains the local code is a valid member of the domain, so that local codes in CWE domains constitute neither an error nor an exceptional (NULL/other) value in the sense of this specification.
|
2.32.4
Code System Name : ST, inherited from CV
Definition: The common name of the coding system.
The code system name has no computational value. The purpose of a code system name is to assist an unaided human interpreter of a code value to interpret codeSystem. It is suggested — though not absolutely required — that ITS provide for codeSystemName in order to annotate the UID for human comprehension.
HL7 systems must not functionally rely on codeSystemName. codeSystemName can never modify the meaning of codeSystem and cannot exist without codeSystem.
|
Definition: The common name of the coding system.
The code system name has no computational value. The purpose of a code system name is to assist an unaided human interpreter of a code value to interpret codeSystem. It is suggested — though not absolutely required — that ITS provide for codeSystemName in order to annotate the UID for human comprehension.
HL7 systems must not functionally rely on codeSystemName. codeSystemName can never modify the meaning of codeSystem and cannot exist without codeSystem.
|
2.32.5
Code System Version : ST, inherited from CV
Definition: If applicable, a version descriptor defined specifically for the given code system.
HL7 shall specify how these version strings are formed for each external code system. If HL7 has not specified how version strings are formed for a particular coding system, version designations have no defined meaning for such coding system.
Different versions of one code system must be compatible. Whenever a code system changes in an incompatible way, it will constitute a new code system, not simply a different version, regardless of how the vocabulary publisher calls it.
For example, the publisher of ICD-9 and ICD-10 calls these code systems, "revision 9" and "revision 10" respectively. However, ICD-10 is a complete redesign of the ICD code, not a backward compatible version. Therefore, for the purpose of this data type specification, ICD-9 and ICD-10 are different code systems, not just different versions. By contrast, when LOINC updates from revision "1.0j" to "1.0k", HL7 would consider this to be just another version of LOINC, since LOINC revisions are backwards compatible.
|
Definition: If applicable, a version descriptor defined specifically for the given code system.
HL7 shall specify how these version strings are formed for each external code system. If HL7 has not specified how version strings are formed for a particular coding system, version designations have no defined meaning for such coding system.
Different versions of one code system must be compatible. Whenever a code system changes in an incompatible way, it will constitute a new code system, not simply a different version, regardless of how the vocabulary publisher calls it.
For example, the publisher of ICD-9 and ICD-10 calls these code systems, "revision 9" and "revision 10" respectively. However, ICD-10 is a complete redesign of the ICD code, not a backward compatible version. Therefore, for the purpose of this data type specification, ICD-9 and ICD-10 are different code systems, not just different versions. By contrast, when LOINC updates from revision "1.0j" to "1.0k", HL7 would consider this to be just another version of LOINC, since LOINC revisions are backwards compatible.
|
2.32.6
Display Name : ST, inherited from CV
Definition: A name or title for the code, under which the sending system shows the code value to its users.
displayName is included both as a courtesy to an unaided human interpreter of a code value and as a documentation of the name used to display the concept to the user. The display name has no functional meaning; it can never exist without a code; and it can never modify the meaning of code.
NOTE: HL7 offers a "print name" in it's predefined vocabulary domains. These values are suitable for use in the displayName.
NOTE: Display names may not alter the meaning of the code value. Therefore, display names should not be presented to the user on a receiving application system without ascertaining that the display name adequately represents the concept referred to by the code value. Communication must not simply rely on the display name. The display name's main purpose is to support debugging of HL7 protocol data units (e.g., messages.)
|
Definition: A name or title for the code, under which the sending system shows the code value to its users.
displayName is included both as a courtesy to an unaided human interpreter of a code value and as a documentation of the name used to display the concept to the user. The display name has no functional meaning; it can never exist without a code; and it can never modify the meaning of code.
NOTE: HL7 offers a "print name" in it's predefined vocabulary domains. These values are suitable for use in the displayName.
NOTE: Display names may not alter the meaning of the code value. Therefore, display names should not be presented to the user on a receiving application system without ascertaining that the display name adequately represents the concept referred to by the code value. Communication must not simply rely on the display name. The display name's main purpose is to support debugging of HL7 protocol data units (e.g., messages.)
|
2.32.7
Original Text : ED, inherited from CV
Definition: The text or phrase used as the basis for the coding.
The original text exists in a scenario where an originator of the information does not assign a code, but where the code is assigned later by a coder (post-coding.) In the production of a concept descriptor, original text may thus exist without a code.
NOTE: Although post-coding is often performed from free text information, such as documents, scanned images or dictation, multi-media data is explicitly not permitted as original text. Also, the original text property is not meant to be a link into the entire source document. The link between different artifacts of medical information (e.g., document and coded result) is outside the scope of this specification and is maintained elsewhere in the HL7 standards. The original text is an excerpt of the relevant information in the original sources, rather than a pointer or exact reproduction. Thus the original text is to be represented in plain text form.
Values of type may have a non-NULL original text property despite having a NULL code. Any value with code of NULL signifies a coding exception. In this case, originalText is a name or description of the concept that was not coded. Such exceptional values may also contain translations. Such translations directly encode the concept described in originalText.
A can be demoted into an ST value representing only the originalText of the value.
|
Definition: The text or phrase used as the basis for the coding.
The original text exists in a scenario where an originator of the information does not assign a code, but where the code is assigned later by a coder (post-coding.) In the production of a concept descriptor, original text may thus exist without a code.
NOTE: Although post-coding is often performed from free text information, such as documents, scanned images or dictation, multi-media data is explicitly not permitted as original text. Also, the original text property is not meant to be a link into the entire source document. The link between different artifacts of medical information (e.g., document and coded result) is outside the scope of this specification and is maintained elsewhere in the HL7 standards. The original text is an excerpt of the relevant information in the original sources, rather than a pointer or exact reproduction. Thus the original text is to be represented in plain text form.
Values of type may have a non-NULL original text property despite having a NULL code. Any value with code of NULL signifies a coding exception. In this case, originalText is a name or description of the concept that was not coded. Such exceptional values may also contain translations. Such translations directly encode the concept described in originalText.
A can be demoted into an ST value representing only the originalText of the value.
|
2.33
Monetary Amount (MO) specializes QTY
Definition: An MO is a quantity expressing the amount of money in some currency. Currencies are the units in which monetary amounts are denominated in different economic regions. While the monetary amount is a single kind of quantity (money) the exchange rates between the different units are variable. This is the principle difference between PQ and MO, and the reason why currency units are not physical units.
|
2.33.1
Value : REAL
Definition: The magnitude of the MO in terms of currency.
NOTE: MO values are usually precise to 0.01 (one cent, penny, paisa, etc.) For large amounts, it is important not to store MO values in floating point registers, since this may lose precision. However, this specification does not define the internal storage of REAL as fixed or floating point numbers.
REAL.precision is the precision of the decimal representation, not the precision of the value. REAL has no notion of uncertainty or accuracy. For example, "1.99 USD" (precision 3) times 7 is "13.93 USD" (precision 4) and should not be rounded to "13.9" to keep the precision constant.
2.33.2
Currency : CS
Definition: The currency unit as defined in ISO 4217.
This table only shows a representative subset of the codes defined by ISO 4217. All codes from ISO 4127 are valid for this attribute
2.33.3
Equality : BL, inherited from ANY
Two MO values are equal if both value and currency are equal.
|
2.33.4
Comparability : BL, inherited from QTY
Two MO values can be compared to each other (and have an ordering and difference) if their currencys are equal.
If their currencys are not identical, the values cannot be compared. Conversion between currencies is outside the scope of this specification. In practice, foreign exchange rates are highly variable not only over long and short amounts of time, but also depending on location and access to currency trade markets.
|
2.33.5
DifferenceDataType : TYPE, inherited from QTY
|
The difference between 2 MOs is another MO.
2.33.6
Addition : MO
Definition: Two MOs can be added if their currencys are equal.
|
2.33.7
Real Multiplication : MO
Definition: Multiplication with a REAL forms a scaled quantity. A scaled quantity is comparable to its original quantity.
|
2.33.8
Literal Form
The literal form for an MO consists of a currency code string, optional whitespace, and a REAL literal amount.
|
For example, "USD189.95" is the literal for 189.95 U.S. Dollar.
2.34
Calendar (CAL) specializes SET<CLCY>
Definition: A calendar is a concept of measuring time in various cycles. Such cycles are years, months, days, hours, minutes, seconds, and weeks. Some of these cycles are synchronized and some are not (e.g., weeks and months are not synchronized.)
After "rolling the time axis" into these cycles a calendar expresses a point in time as a sequence of integer counts of cycles, e.g., for year, month, day, hour, etc. The calendar is rooted in some conventional start point, called the "epoch."
A calendar "rolls" the time axis into a complex convolute according to the calendar periods year (blue), month (yellow), day (green), hour (red), etc. The cycles need not be aligned, for example, the week (not shown) is not aligned to the month.46
Calendar is defined as a set of calendar cycles, and has a name and a code. The head of the Calendar is the largest CalendarCycle appearing right most in the calendar expression. The epoch is the beginning of that calendar, i.e., the point in time where all calendar cycles are zero.
|
The calendar definition can be shown as in Table 36 for the modern Gregorian calendar. The calendar definition table lists a calendar cycle in each row. The calendar units are dependent on each other and defined in the value column. The sequence column shows the relationship through the next property. The other columns are as in the formal calendar cycle definition.47
2.35
Calendar Cycle (CLCY) specializes ANY
Definition: A calendar cycle defines one group of decimal digits in the calendar expression. Examples for calendar cycles are year, month, day, hour, minute, second, and week.
A calendar cycle has a name and two codes, a one-letter code and a two-letter code. The property ndigits is the number of decimal digits occupied in the calendar expression. The property start specifies where counting starts (i.e., at 0 or 1.) The next property is the next lower cycle in the order of the calendar expression. The max(t) property is the maximum number of cycles at time t (max depends on the time t to account for leap years and leap seconds.) The property value(t) is the integer number of cycles shown in the calendar expression of time t. The property sum(t, n) is the sum of n calendar cycles added to the time t.
|
2.36
Point in Time (TS) specializes QTY
Definition: A quantity specifying a point on the axis of natural time. A point in time is most often represented as a calendar expression.
Semantically, however, time is independent from calendars and best described by its relationship to elapsed time (measured as a physical quantity in the dimension of time). A TS plus an elapsed time yields another TS. Inversely, a TS minus another TS yields an elapsed time.
As nobody knows when time began, a TS is conceptualized as the amount of time that has elapsed from some arbitrary zero-point, called an epoch. Because there is no absolute zero-point on the time axis; natural time is a difference-scale quantity, where only differences are defined but no ratios. (For example, no TS is — absolutely speaking — "twice as late" as another TS.)
Given some arbitrary zero-point, one can express any point in time as an elapsed time measured from that offset. Such an arbitrary zero-point is called an epoch. This epoch-offset form is used as a semantic representation here, without implying that any system would have to implement TS in that way. Systems that do not need to compute distances between TSs will not need any other representation than a calendar expression literal.
|
2.36.1
Offset from Epoch : PQ
Definition: The elapsed time since any constant epoch, measured as a physical quantity in the dimension of time (i.e., comparable to one second.)
|
It is not necessary for this specification to define a canonical epoch; the semantics is the same for any epoch, as long as the epoch is constant.
NOTE: offset may be treated as a purely semantic property that is not represented in any way other than the calendar literal expression. However, an ITS may just as well choose to define a constant epoch and represent TS values as elapsed time offsets relative to that epoch. However, an ITS using an epoch-offset representation would still need to communicate the calendar code and the precision of a calendar representation once other calendars are supported.
2.36.2
Equality : BL, inherited from QTY
Two TS values are equal if and only if their offsets (relative to the same epoch) are equal.
|
2.36.3
Calendar : CS
Definition: A code specifying the calendar used in the literal representation of this TS.48
The purpose of this property is mainly to faithfully convey what has been entered or seen by a user in a system originating such a TS value. calendar also advises any system rendering a TS value into a literal form of which calendar to use. However, this is only advice; any system that renders TS values to users may choose to use the calendar and literal form demanded by its users rather than the calendar mentioned in calendar. Hence, calendar is not constant in communication between systems, the calendar is not part of the equality test.
For the purpose of defining the relationship between calendar expression and epoch/offset form, two private data types, CAL and CLCY are defined. These calendar data types exist only for defining this specification. These private data types may not be used at all outside this specification.
2.36.4
Precision of the Calendar Literal Form : INT
Definition: The number of significant digits of the calendar expression representation.
precision is formally defined based on the literal.
precision is only the precision of a decimal digit representation, not the accuracy of the TS value.
The purpose of precision is to faithfully capture the whole information presented to humans in a calendar expression. The number of digits shown conveys information about the uncertainty (i.e., precision and accuracy) of a measured TS.
NOTE: The precision of the representation is independent from uncertainty (precision accuracy) of a measurement result. If the uncertainty of a measurement result is important, one should specify uncertain values as PPD
precision is dependent on calendar. A given precision relative to one calendar does not mean the same in another calendar with different periods.
For example "20000403" has 8 significant digits in the representation, but the uncertainty of the value may be in any digit shown or not shown, i.e., the uncertainty may be to the day, to the week, or to the hour. Note that external representations should adjust their representational precision with the uncertainty of the value. However, since the precision in the digit string depends on the calendar and is granular to the calendar periods, uncertainty may not fall into that grid (e.g., 2000040317 is an adequate representation for the value between 2000040305 and 2000040405.)
NOTE: A character based ITS need not represent precision as an explicit attribute if TS values are represented as literal calendar expressions. A TS representation must not produce more or less significant digits than were originally in that value. Conformance can be tested through round-trip encoding - decoding - encoding.
2.36.5
Timezone Offset : PQ
Definition: The difference between the local time in that time zone and Universal Coordinated Time (UTC, formerly called Greenwich Mean Time, GMT). The time zone is a PQ in the dimension of time (i.e., comparable to one second.) A zero time zone value specifies UTC. The time zone value does not permit conclusions about the geographical longitude or a conventional time zone name.
For example, 200005121800-0500 may be eastern standard time (EST) in Indianapolis, IN, or central daylight savings time (CDT) in Decatur, IL. Furthermore in other countries having other latitude the time zones may be named differently.
|
When timezone is NULL (unknown), "local time" is assumed. However, "local time" is always local to some place, and without knowledge of that place, the time zone is unknown. Hence, a local time cannot be converted into UTC. timezone should be specified for all TS values in order to avoid a significant loss of precision when TSs are compared. The difference of two local times where the locality is unknown has an error of ±12 hours.
In administrative data context, some time values do not carry a time zone. For a date of birth in administrative data, for example, it would be incorrect to specify timezone, since this may effectively change the date of birth when converted into other time zones. For such administrative data the time zone is NULL (not applicable.)
2.36.6
DifferenceDataType : TYPE, inherited from QTY
|
The difference between 2 TSs is a PQ in the dimension of time.
2.36.7
Addition : TS, inherited from QTY
Definition: A TS plus an elapsed time (i.e., PQ in the dimension of time) is a TS.
|
2.36.8
Difference : QTY, inherited from QTY
Definition: The difference between two TSs is an elapsed time.
|
2.36.9
Literal Form
TS literals are simple calendar expressions, as defined by the calendar definition table. By default, the western (Gregorian) calendar shall be used (Table 36).
For the default Gregorian calendar the calendar expression literals of this specification conform to the constrained ISO 8601 that is defined in ISO 8824 (ASN.1) under clause 32 (generalized time) and to the HL7 Version 2 TS data type.
Calendar expression literals are sequences of integer numbers ordered according to the "counter" column of Table 36. Periods with lower order numbers stand to the left of periods with higher order numbers. Periods with no assigned order number cannot occur in the calendar expression for TS.
The "digits" column of Table 36 specifies the exact number of digits for the counter number for any period.
Thus, Table 36 specifies that western calendar expressions begin with the 4-digit year (beginning counting at zero); followed by the 2-digit month of the year (beginning counting at one); followed by the 2-digit day of the month (beginning with one); followed by the 2-digit hour of the day (beginning with zero); and so forth. For example, "200004010315" is a valid expression for April 1, 2000, 3:15 am.
A calendar expression can be of variable precision, omitting parts from the right.
For example, "20000401" is precise only to the day of the month.
The least defined calendar period (i.e. the second) may be written as a REAL, with the number of integer digits specified, followed by the decimal point and any number of fractional digits.
For example, "20000401031520.34" means April 1, 2000, 3:15 and 20.34 seconds.
When other calendars are used in the future, a prefix "GREG:" can be placed before the western (Gregorian) calendar expression to disambiguate from other calendars. Each calendar shall have its own prefix. However, the western calendar is the default if no prefix is present.
In the modern Gregorian calendar (and all calendars where time of day is based on UTC), the calendar expression may contain a time zone suffix. The time zone suffix begins with a plus (+) or minus (-) followed by digits for the hour and minute cycles. UTC is designated as offset "+00" or "-00"; the ISO 8601 and ISO 8824 suffix "Z" for UTC is not permitted.
|
3
Generic Collections
This section defines data types that can "collect" other data values, Set, Sequence, Bag and Interval.49 These collection types are defined as generic (parameterized) types. The concept of generic types is described in Generic Data Types (§ 1.9.5 ).
3.1
Set (SET) specializes ANY
Definition: A value that contains other distinct values in no particular order.
3.1.1
Contains Element : BL
Definition: A relation of the set with its elements, true if the given value is an element of the set.
This is the primitive semantic property of a set, based on which all other properties are defined.
A set may only contain distinct non-NULL elements. Exceptional values (NULL-values) cannot be elements of a set.
|
3.1.2
Contains Subset : BL
Definition: The relation between a set and its subsets, where each element in the subset is also an element of the superset.
|
This implies that the empty set is a subset of every set including itself.
3.1.3
Not-Empty : BL
Definition: A predicate indicating that this set contains elements.
|
3.1.4
The Empty Set : BL
Definition: A predicate indicating that this set has no elements (negation of the notEmpty. The empty set is a proper set value, not an exceptional (NULL) value.
|
3.1.5
Cardinality : INT
Definition: The cardinality of a set is the number of distinct elements in the set.
|
The cardinality definition is not sufficient since it doesn't converge for uncountably infinite sets (REAL, PQ, etc.) and it doesn't terminate for infinite sets. In addition, the definition of integer number type in this specification is incomplete for these cases, as it doesn't account for infinities. Finally the cardinality value is an example where it would be necessary to distinguish the cardinality ℵ0 (aleph0) of countably infinite sets (e.g., INT) from ℵ1 (aleph1), the cardinality of uncountable sets (e.g., REAL, PQ).
3.1.6
Union : SET<T>
Definition: A union of two sets (component sets) is a set where each of the union's elements also is an element of either one component set.
|
3.1.7
Include Element : SET<T>
Definition: A union of a set and an element.
|
3.1.8
Set Difference : SET<T>
Definition: The difference of this set and its subtracting set is the set that contains all elements of this set that are not elements of the subtracting set.
|
3.1.9
Exclude Element : SET<T>
Definition: The difference between this set and an element value is the set that contains all elements of this set except for the subtracting element value. If the element value is not contained in this set, the difference is equal to this set.
|
3.1.10
Intersection : SET<T>
Definition: The intersection between two sets is a set containing all and only those elements that are contained in both of the operand sets.
|
3.1.11
Literal Form
When the element type T has a literal form, the set of T elements has a literal form, wherein the elements of the set are enumerated within curly braces and separated by semicolon characters.
|
NOTE: This literal form for sets is only practical for relatively small enumerable sets; this does not mean, however, that all sets are relatively small enumerations of elements.
NOTE: A character-based ITS should choose a different literal form for sets if the Implementation Technology has a more native literal form for such collections.
3.1.12
Promotion of Element Values to Sets : SET<T>
A data value of type T can be promoted into a trivial set of T with that data value as its only element.
|
3.1.13
Convex Hull of Totally Ordered Sets : IVL<T>
Sets of quantities may be totally ordered sets when there is an order relationship defined between any two elements in the set. Note that "ordered set" does not mean the same as Sequence (LIST). For example, the set {3; 2; 4; 88; 1} is an ordered set. The ordering of the elements in the set notation is still irrelevant, but elements can be compared to establish an order (1; 2; 4; 88).
Totally ordered sets have convex hull. A convex hull of a totally ordered set S is the smallest interval that is a superset of S. This concept is going to be important later on.
|
Note that hull is defined if and only if the actual set is a totally ordered set. The data type of the elements itself need not be totally ordered. For example, the data type PQ is only partially ordered (since only quantities of the same kind can be compared), but a SET<PQ> may still be totally ordered (if it contains only comparable quantities.) For example, the convex hull of {4 s, 20 s, 55 s} is [4 s;55 s]; the convex hull of {"apples"; "oranges"; "bananas"} is undefined because the elements have no order relationship among them; and the convex hull of {2 m; 4 m; 8 s} is likewise undefined, because it is not totally ordered (seconds are not comparable with meters.)
3.2
Sequence (LIST) specializes ANY
Definition: A value that contains other discrete (but not necessarily distinct) values in a defined sequence.
A sequence may contain NULL values as items.
3.2.1
Head Item : T
Definition: The first item in this sequence. The head is a definitional property for the semantics of the sequence.
3.2.2
Tail Sequence : LIST<T>
Definition: The sequence following the first item in this sequence. The tail is a definitional property for the semantics of the sequence.
3.2.3
Empty Sequence : BL
Definition: A predicate that is true if this sequence is an empty sequence, i.e., if it contains no items.
Notice the difference between empty-sequence and NULL: an empty sequence is a proper sequence, not a null-value.
|
Notice that head and tail being NULL is only a necessary condition but not sufficient for determining an empty list, since a sequence may contain NULL-values as items, this condition can mean that this list has only a head item that happens to be NULL.
3.2.4
Not-Empty Sequence : BL
Definition: A predicate that is true if this sequence is not-empty. Negation of isEmpty.
|
3.2.5
Item by Index : T
Definition: The item at the given sequential position (index) in the sequence. The index zero refers to the first element (head) of the sequence.
|
3.2.6
Contains Item : BL
Definition: A predicate that is true if this sequence contains the given item value.
|
3.2.7
Length : INT
Definition: The number of elements in the sequence. NULL elements are counted as regular sequence elements.
|
3.2.8
Equality : BL, inherited from ANY
Two lists are equal if and only if they are both empty, or if both their head and their tail are equal.
|
3.2.9
Literal Form
When the element type T has a literal form, the sequence LIST has a literal form. List elements are enumerated, separated by semicolon, and enclosed in parentheses.
|
NOTE: a character-based ITS should choose a different literal form for sequences if the Implementation Technology has a more native literal form for such collections.
3.2.10
Promotion of Item Values to Sequences : LIST<T>
A data value of type T can be promoted into a trivial sequence of T with that data value as its only item.
|
3.3
GeneratedSequence (GLIST) specializes LIST
Definition: A periodic or monotone sequence of values generated from a few parameters, rather than being enumerated. Used to specify regular sampling points for biosignals.
|
The item at a certain index in the list is calculated by performing an integer division on the index (i) with the denominator (d) and then take that value's remainder with the period (p). Multiply this value with the increment (Δx) and add to the head (x0.)
xi=x0 + Δx × (i/d) mod p
|
3.3.1
Head Item : T, inherited from LIST
This is the start-value of the generated list.
3.3.2
Increment : QTY
Definition: The difference between one value and its previous different value. For example, to generate the sequence (1; 4; 7; 10; 13; ...) the increment is 3; likewise to generate the sequence (1; 1; 4; 4; 7; 7; 10; 10; 13; 13; ...) the increment is also 3.
|
3.3.3
Period Step Count : INT
Definition: If non-NULL, specifies that the sequence alternates, i.e., after this many increments, the sequence item values roll over to start from the initial sequence item value. For example, the sequence (1; 2; 3; 1; 2; 3; 1; 2; 3; ...) has period 3; also the sequence (1; 1; 2; 2; 3; 3; 1; 1; 2; 2; 3; 3; ...) has period 3 too.
The period allows to repeatedly sample the same sample space. The "waveform" of this periodic generator is always a "saw", just like the x-function of your oscilloscope.50
3.3.4
Denominator : INT
Definition: The the integer by which the index for the sequence is divided, effectively the number of times the sequence generates the same sequence item value before incrementing to the next sequence item value. For example, to generate the sequence (1; 1; 1; 2; 2; 2; 3; 3; 3; ...) the denominator is 3.
The use of the denominator is to allow multiple generated sequences to periodically scan a multidimensional space. For example, an (abstract) TV screen uses 2 such generators for the columns and rows of pixels. For instance, if there are 200 scan lines and 320 raster colunmns, the column-generator would have denominator 1 and the line-generator would have denominator 320.
3.4
SampledSequence (SLIST) specializes LIST
Definition: A sequence of sampled values scaled and translated from a list of integer values. Used to specify sampled biosignals.
|
The item at a certain index (i) in the list is calculated by multiplying the item at the same index in the digits sequence (di) with the scale (s) and then add that value to the origin (xo).
xi=xo + s × di
|
3.4.1
Scale Origin : T
Definition: The origin of the list item value scale, i.e., the physical quantity that a zero-digit in the sequence would represent.
3.4.2
Scale Factor : QTY
Definition: A ratio-scale quantity that is factored out of the digit sequence.
|
3.4.3
Sampled Digits : LIST<INT>
Definition: A sequence of raw digits for the sample values. This is typically the raw output of an A/D converter.
3.5
Bag (BAG) specializes ANY
Definition: An unordered collection of values, where each value can be contained more than once in the collection.
|
NOTE: A BAG can be represented in two ways. Either as a simple enumeration of elements, including repeated elements, or as a "compressed bag" whereby the content of the BAG is listed in pairs of element value and number. A histogram showing absolute frequencies is a BAG represented in compressed form. BAG is therefore useful to communicate raw statistical data samples.
3.5.1
Contains Item : INT
Definition: The number of items in this bag with the given item value.
This is the primitive semantic property of a BAG, on which all other properties are defined.
|
3.5.2
Not-Empty : BL
Definition: A predicate indicating that this BAG contains item.
|
3.5.3
The Empty Bag : BL
Definition: A predicate indicating that this BAG has no elements (negation of the notEmpty predicate. The empty BAG is a proper value, not an exceptional (NULL) value.
|
3.5.4
Addition : BAG<T>
Definition: A BAG that contains all items of the operand BAGs, i.e. the number of items of each item value are added.
|
3.5.5
Subtraction : BAG<T>
Definition: A BAG that contains all items of this BAG (minuend) diminished by the items in the other BAG (subtrahend). BAGs cannot carry deficits. When the subtrahend contains more items of one value than the minuend, the difference contais zero items of that value.
|
3.5.6
Promotion of Item Values to Bags : BAG<T>
A data value of type T can be promoted into a trivial BAG of type T with that data value as its only item.
|
3.6
Interval (IVL) specializes SET
Definition: A set of consecutive values of an ordered base data type.
Any ordered type can be the basis of an IVL; it does not matter whether the base type is discrete or continuous. If the base data type is only partially ordered, all elements of the IVL must be elements of a totally ordered subset of the partially ordered data type.
For example, PQ is considered ordered. However the ordering of PQs is only partial; a total order is only defined among comparable quantities (quantities of the same physical dimension.) While IVLs between 2 and 4 meter exists, there is no IVL between 2 meters and 4 seconds.
IVLs are SETs and have all the properties of SETs. However, union and difference of SETs may not be SETs, since the elements of these union and difference SETs might not be contiguous. Intersections of SETs are always SETs.
3.6.1
Low Boundary : T
Definition: This is the low limit.
|
3.6.2
High Boundary : T
Definition: This is the high limit.
|
3.6.3
Width : QTY
Definition: The difference between high and low boundary. The purpose of distinguishing width is to handle all cases of incomplete information symmetrically. In any SET representation only two of the three properties high, low, and width need to be stated and the third can be derived.
When both boundaries are known, width can be derived as high minus low. When one boundary and width is known, the other boundary is also known. When no boundary is known, width may still be known. For example, one knows that an activity takes about 30 minutes, but one may not yet know when that activity is started.
Note that the data type of width is not always the same as for the boundaries. For ratio scale quantities (REAL, PQ, MO) it is the same. For difference scale quantities (e.g., TS) is the data type of the difference (e.g., PQ in the dimension of time for TS). For discrete elements (INT) the width may be a REAL indicating the number of elements in the interval divided by 2.
|
3.6.4
Central Value : T
Definition: The arithmetic mean of the IVL (low plus high divided by 2). The purpose of distinguishing center as a semantic property is for conversions of IVLs to and from point values.
Note that center doesn't always exist for every IVL. Notably IVLs that are infinite on one side do not have center. Also IVLs of discrete base types with an even number of elements do not have a center. If an IVL is unknown on one (or both) boundaries, center can still be asserted. In fact, the main use case for center is to be asserted when no boundary is known.
|
3.6.5
Low Boundary Closed : BL
Definition: Specifies whether low is included in the IVL (is closed) or excluded from the IVL (is open).
|
3.6.6
High Boundary Closed : BL
Definition: Specifies whether high is included in the IVL (is closed) or excluded from the IVL (is open).
|
3.6.7
Literal Form
The literal form for IVL is defined such that it is as intuitive to humans as possible. Five different forms are defined:51
- the interval form using square brackets, e.g., "[3.5; 5.5[";
- the dash-form, e.g., "3.5-5.5";
- the "comparator" form, using relational operator symbols, e.g., "<5.5";
- the center-width form, e.g., "4.5[2.0[".
- the width-only form using square brackets, e.g., "[2.0[".
|
3.6.8
Promotion of Element Values to Intervals : IVL<T>
A quantity of type T can be promoted into a trivial IVL where low and high are equal and boundaries closed.
|
3.6.9
Demotion of Intervals to a Representative Element Value : T
An IVL can be demoted to a simple quantity of type T that is representative for the whole IVL. If both boundaries are finite, this is the center. If one boundary is infinite, the representative value is the other boundary. If both boundaries are infinite, the conversion to a point value is not applicable.
|
3.6.10
Convex Hull : IVL<T>, inherited from SET
Definition: A convex hull or "interval hull" of two IVLs is the least IVL that is a superset of its operands.

Convex Hull of two Intervals
|
3.7
Interval of Physical Quantities (IVL<PQ>) specializes IVL
Definition: A set of consecutive values of physical quantities.
An interval of physical quantities is constructed from the generic interval type. However, recognizing that the unit can be factored from the boundaries, we add additional semantics and a separate literal form. The additional view of an interval of physical quantities is an interval of real numbers with one unit.
|
The unit applies to both low and high boundary.
|
The special literal form is simply an interval of real numbers a space and the unit.
|
For example: "[0;5] mmol/L" or "<20 mg/dL" are valid literal forms of intervals of physical quantities. The generic interval form, e.g., "[50 nm; 2 m]" is also allowed.
3.8
Interval of Point in Time (IVL<TS>) specializes IVL
Definition: A set of consecutive values of time-stamps.
The generic interval data type defines the interval of points in time too. However, there are some special considerations about literal representations and conversions of intervals of point in time, which are specified in this section.
|
3.8.1
Promotion of Points in Time Values to Intervals : IVL<TS>, inherited from IVL
A TS can be promoted to an IVL<TS> whereby the low boundary is the TS value itself, and the width is inferred from the precision of the TS and the duration of the least significant calendar period specified. The high boundary is open. For example, the TS literal "200009" is converted to an IVL<TS> with low boundary 200009 and width 30 days, which is the interval "[200009;200010[".
3.8.2
Literal Form
The literal form for interval of point in time is exceptional.
- The "dash form" is not allowed for intervals of point in time
- A "hull form" is defined instead
In order to avoid syntactic conflicts with the timezone and slightly different usage profiles of the ISO 8601 that occur on some ITS platforms, the dash form of the interval is not permitted forIVL<TS>. The interval-form using square brackets is preferred.
Example: May 12, 1987 from 8 to 9:30 PM is
"[198705122000;198705122130]".
NOTE: The precision of a stated interval boundary is irrelevant for the interval. One might wrongly assume that the interval "[19870901;19870930]" stands for the entire September 1987 until end of the day of September 30. However, this is not so! The proper way to denote an entire calendar cycle (e.g., hour, day, month, year, etc.) in the interval notation with is to use an open high boundary. For example, all of September 1987 is denoted as "[198709;198710[".52
The "hull-form" of the literal is defined as the convex hull (see IVL.hull) of interval-promotions from two time stamps.
|
For example, "19870901..19870930" is a valid literal
using the hull form. The value is equivalent to the interval form
"[19870901;19871001[".53
The hull-form further allows an abbreviation, where the higher timestamp literal does not need to repeat digits on the left that are the same as for the lower timestamp literal. The two timestamps are right-aligned and the digits to the left copied from the lower to the higher timestamp literal. This is a simple string operation and is not formally defined here.
Example: May 12, 1987 to May, 23, 1987 is
"19870512..23". However, note that May 12, 1987 to June
2, 1987 is "19870512..0602", and not
"20000512..02".
4
Generic Type Extensions
Generic type extensions are generic types with one parameter type, and that extend (specialize) their parameter type. In the formal data type definition language, generic type extensions follow the pattern: template<ANY T> typeGenericTypeExtensionNamespecializes T { ... }; These generic type extensions inherit most properties of their base type and add some specific feature to it. The generic type extension is a specialization of the base type, thus a value of the extension data type can be used instead of its base data type.
NOTE: Values of extended types can be substituted for their base type. However, an ITS may make some constraints as to what extensions to accommodate. Particularly, extensions need not be defined for those components carrying the values of data value properties. Thus, while any data value can be annotated outside the data type specification, and ITS may not provide for a way to annotate the value of a data value property. At this time HL7 does not permit use of generic type extensions, except where explicitly enabled (in this or another HL7 specification) for such use cases where this advanced functionality is important. In these cases, instances of these generic type extensions must be specifically and explicitly reflected in the HL7 RIM, MIM, RMIM and HMD (as applicable), as a result of balloted Technical Committee content.54
4.1
History Item (HXIT) specializes T
Definition: A generic data type extension that tags a time range to any data value of any data type. The time range is the time in which the information represented by the value is (was) valid.
If the base type T does not possess a validTime property, the HXIT adds that property to the base type. If, however, the base type T does have a valid time property (currently only EN), that property is mapped to the valid time property of the HXIT55
|
4.1.1
Valid Time : IVL<TS>
Definition: The time interval during which the given information was, is, or is expected to be valid. The interval can be open or closed infinite or undefined on either side.
4.2
History (HIST) specializes SET<HXIT>
Definition: A set of data values that have a valid-time property and thus conform to the HXIT type. The history information is not limited to the past; expected future values can also appear.
The intent of the HIST data type is to capture the true historical (and future) values of an item, rather than the audit trail of values any given system has held for the item.
|
The semantics does not principally forbid the time intervals to overlap. However, if two history items have the same IVL.low and IVL.high boundaries in the valid time interval, it is undefined which one is considered the earliest (latest).
|
4.2.1
Earliest Item : HXIT<T>
Definition: The item in the set whose IVL.low boundary (validity start time) is less than or equal to (i.e. before) that of any other history item in the set.
|
4.2.2
Latest Item : HXIT<T>
Definition: The item in the set whose IVL.high boundary (validity end time) is greater than or equal to (i.e. after) that of any other history item in the set.
|
4.2.3
Except Earliest Item : HIST<T>
Definition: The derived history that has the earliest item excluded.
|
4.2.4
Except Latest Item : HIST<T>
Definition: The derived history that has the latest item excluded.
|
4.2.5
Demotion of a History to a Single History Item : HXIT<T>
A type conversion between an entire history HIST and a single history item HIST. This conversion takes the latest data from the history.
The purpose of this conversion is to allow an information producer to produce a history of any value instead of sending just one value. An information-consumer, who does not expect a history but a simple value, will convert the history to the latest value.
Note, from the definition of HXIT, that HXIT semantically specializes T. This means, that the information-consumer expecting a T but given an HXIT will not recognize any difference (substitutability of specializations.)
4.3
Uncertain Value - Probabilistic (UVP) specializes T
Definition: A generic data type extension used to specify a probability expressing the information producer's belief that the given value holds.
How the probability number was arrived at is outside the scope of this specification.
Probabilities are subjective and (as any data value) must be interpreted in their individual context, for example, when new information is found the probability might change. Thus, for any message (document, or other information representation) the information — and particularly the probabilities — reflect what the information producer believed was appropriate for the purpose and at the time the message (document) was created.
For example, at the beginning of the 2000 baseball season (May), the Las Vegas odds makers may have given the New York Yankees a probability of 1 in 10 (0.100) of winning the World Series. At the time of this writing, the Yankees and Mets have won their respective pennants, but the World Series has yet to begin. The probability of the Yankees winning the World Series is obviously significantly greater at this point in time, perhaps 6 in 10 (0.600). The context, and in particular the time of year, made all the difference in the world.
Since probabilities are subjective measures of belief, they can be stated without being "correct" or "incorrect" per se, let alone "precise" or "imprecise". Notably, one does not have to conduct experiments to measure a frequency of some outcome in order to specify a probability. In fact, whenever statements about individual people or events are made, it is not possible to confirm such probabilities with "frequentists" experiments.
Returning to our example, the Las Vegas odds makers can not insist on the Yankees and Mets playing 1000 trial games prior to the Series; even if they could, they would not have the fervor of the real Series and therefore not be accurate. Instead, the odds makers must derive the probability from past history, player statistics, injuries, etc.
|
The type T is not formally constrained. In theory, discrete probabilities can only be stated for discrete data values. Thus, generally UVP should not be used with REAL, PQ, or MO values.
4.3.1
Probability : REAL
Definition: The probability assigned to the value, a decimal number between 0 (very uncertain) and 1 (certain), inclusive.
|
There is no "default probability" that one can assume when the probability is unstated. Therefore, it is impossible to make any semantic difference between an UVP without probability and a simple T. UVP does not mean "uncertain", and a simple T does not mean "certain". In fact, the probability of the UVP could be 0.999 or 1, which is quite certain, where a simple T value could be a very vague guess.
4.4
Non-Parametric Probability Distribution (NPPD) specializes SET<UVP>
Definition: A set of UVP with probabilities (also known as a histogram.) All the elements in the set are considered alternatives and are rated each with its probability expressing the belief (or frequency) that each given value holds.
The purpose of NPPD is chiefly to support statistical data reporting as it occurs in measurements taken from many subjects and consolidated in a histogram. This occurs in epidemiology, veterinary medicine, laboratory medicine, but also in cost controlling and business process engineering.
Semantically, the information of a stated value exists in contrast to the complement set of unstated possible values. Thus, semantically, an NPPD contains all possible values and assigns probabilities to each of them.
The easiest way to visualize this is a bar chart as shown in
Example of a Histogram
This example illustrates the probability of selected major league baseball teams winning the World Series (prior to the season start). Each team is mutually exclusive, and were we to include all of the teams, the sum of the probabilities would equal 1 (i.e., it is certain that one of the teams will win).
NOTE: Even though semantically NPPD assigns probabilities to all possible values, not all values need to be represented explicitly. Those possible values that are not mentioned will have the remaining probability distributed equally over all unmentioned values. For example, if the value set is {A; B; C; D} but the NPPD value states just {(B; 0.5); (C; 0.25)} then the remaining probability is 1 - 0.75 = 0.25, which is distributed evenly over the complement set: {(A; 0.125); (D; 0.125)}. Semantically, the NPPD is the union of the stated probability distribution and the unstated complement with the remaining probability distributed evenly.
|
Just as with UVP, the type T is not formally constrained, even though there are reasonable and unreasonable uses. Typically one would use NPPD for unordered types, if only a "small" set of possible values is assigned explicit probabilities, or if the probability distribution cannot (or should not) be approximated with parametric methods. For other cases, one may prefer PPD.
4.4.1
Most Likely : UVP
|
5
Timing Specification
The timing specification suite of data types is used to specify the complex timing of events and actions such as those that occur in order management and scheduling systems. It also supports the cyclical validity patterns that may exist for certain kinds of information, such as phone numbers (evening, daytime), office hours, and addresses of so called "snowbirds" (i.e. people who choose to reside closer to the equator during winter and farther from the equator during summer.)
The timing specification data types include point in time (TS) and the interval of time (IVL<TS>) and add types that are specifically suited to repeated schedules. These additional types include PIVL, EIVL, and finally GTS type itself. All these timing types describe the time distribution of repeating states or events.
5.1
Periodic Interval of Time (PIVL) specializes SET
Definition: An interval of time that recurs periodically. PIVL has two properties, phase and period. phase specifies the "interval prototype" that is repeated every ..
For example, "every eight hours for two minutes" is a PIVL where the interval's IVL.width equals 2 minutes and the period at which the interval recurs equals 8 hours.
phase also marks the anchor point in time for the entire series of periodically recurring intervals. The recurrence of a PIVL has no beginning or ending, but is infinite in both future and past.
|
A PIVL is fully specified when both period and phase are fully specified. The interval may be only partially specified where either only IVL.width or only one boundary is specified.
For example: "every eight hours for two minutes" specifies only period and IVL.width of phase but no boundary of the phase. Conversely, "every eight hours starting at 4 o'clock" specifies only period and IVL.low of phase but not IVL.high of phase. "Every eight hours for two minutes starting at 4 o'clock" is fully specified since period, and both IVL.low and IVL.width of phase are specified.
PIVL is a generic type extension whose type parameter T is restricted to a TS and its extensions. PPD<TS>> is an extension of TS and therefore can be used to form PIVL<PPD<TS>> values.
Often times, repeating schedules are only approximately specified. For instance "three times a day for ten minutes each" does not usually mean a period of precisely 8 hours and does often not mean exactly 10 minutes intervals. Rather the distance between each occurrence may vary as much as between 3 and 12 hours and the IVL.width of the interval may be less than 5 minutes or more than 15 minutes. PIVL<PPD<TS>> can be used to indicate how much leeway is allowed or how "timing-critical" the specification is.
5.1.1
Phase : IVL<T>
Definition: A prototype of the repeating interval, specifying the duration of each occurrence and anchors the PIVL sequence at a certain point in time.
phase also marks the anchor point in time for the entire series of periodically recurring intervals. The recurrence of a PIVL has no begin or end but is infinite in both future and past. IVL.width of phase must be less than or equal to period.
|
5.1.2
Period : T.diff
Definition: A time duration specifying as a reciprocal measure of the frequency at which the PIVL repeats.
period is a QTY in the dimension of time (T.diff). For an uncertain PIVLperiod is a probability distribution over elapsed time.
|
5.1.3
Alignment to the Calendar : CS
Definition: Specifies if and how the repetitions are aligned to the cycles of the underlying calendar (e.g., to distinguish every 30 days from "the 5th of every month".) A non-aligned PIVL recurs independently from the calendar. An aligned PIVL is synchronized with the calendar.
For example, "every 5th of the month" is a calendar aligned PIVL. period varies from 28 to 31 days depending on the calendar month. Conversely, "every 30 days" is an independent period that will fall on a different date each month.
The calendar alignment specifies a calendar cycle to which the PIVL is aligned. The even flow of time will then be partitioned by the calendar cycle. The partitioning is called the calendar "grid" generated by the aligned-to calendar cycle. The boundaries of each occurrence interval will then have equal distance from the earliest point in each partition. In other words, the distance from the next lower grid-line to the beginning of the interval is constant.
For example, with "every 5th of the month" the alignment
calendar cycle would be month of the year (MY). The even
flow of time is partitioned in months of the year. The distance
between the beginning of each month and the beginning of its
occurrence interval is 4 days (4 days because day of month (DM) starts
counting with 1.) Thus, as months differ in their number of days, the
distances between the recurring intervals will vary slightly, so that
the interval occurs always on the 5th.
5.1.4
Institution Specified Timing : BL
Definition: Indicates whether the exact timing is up to the party executing the schedule (e.g., to distinguish "every 8 hours" from "3 times a day".)
For example, with a schedule "three times a day" the average time between repetitions is 8 hours, however, with institution specified time indicator equal to true, the timing could follow some rule made by the executing person or organization ("institution"), that, e.g., three times a day schedules are executed at 7 am, noon, and 7 pm.
5.1.5
Literal Form
Generic Literal Form. The generic literal form for periodic intervals of time is as follows:
(phase : IVL<T>( / (period : QTY ( [ @ (alignment( ] [ IST ].
|
For example, "[200004181100;200004181110]/(7 d)@DW"
specifies every Tuesday from 11:00 to 11:10 AM. Conversely,
"[200004181100;200004181110]/(1 mo)@DM" specifies every
18th of the month 11:00 to 11:10 AM.
See Table 36 for calendar-period codes defined for the Gregorian calendar. There are 1-character and 2-character symbols. The 2-character symbols are preferred for the alignment.
Calendar Pattern Form. This form is used to specify calendar-aligned timing more intuitively using "calendar patterns." The calendar pattern syntax is (semi-formally) defined as follows:
(anchor( [ (calendar digits( [ .. (calendar digits( ]] / (number : INT( [ IST ]
A calendar pattern is a calendar date where the higher significant digits (e.g., year and month) are omitted. In order to interpret the digits, a period identifier is prefixed that identifies the calendar period of the left-most digits. This calendar period identifier anchors the calendar digits following to the right.
See Table 36 for calendar-period codes defined for the Gregorian calendar. There are 1-character and 2-character symbols. The 1-character symbols are preferred for the calendar pattern anchor.
For example: "M0219" is February 19 the entire day every
year. This periodic interval has the February 19 of any year as its
phase (e.g., "[19690219;19690220[" ), a period of one
year, and alignment month of the year (M). The alignment
calendar-cycle is the same as the anchor (e.g., in this example, month
of the year.)
The calendar digits may also omit digits on the right. When digits are
omitted on the right, this means the interval from lowest to highest
for these digits. For example, "M0219" is February 19 the
entire day; "M021918" is February 19, the entire hour
between 6 and 7 PM.
In absence of a formal definition for this, the rules for parsing a
calendar pattern are as follows (example is "M021918..21"):
-
read the anchoring period identifier (e.g. "
M") - alignment is equal to this calendar period (e.g. month of the year)
-
use the current point in time and format a literal exact to the next
higher significant calendar period from the anchoring calendar period
(e.g. year, "
2000", constructing "2000021918"); this is the "stem literal" -
read this constructed literal (e.g., "
2000021918") into a TS value and convert that value to an interval according to IVL_TS.promotionTS (e.g., "[2000021918;2000021919[") this is the "low interval." - if the hull-operator token ".." follows, read the following calendar digits (e.g., "21")
-
right-align the stem literal and the calendar digits just read
"2000021918" " 21" -
and copy all digits from the stem literal that are missing to the left
of the calendar digits just read (e.g., yields "
2000021921".) -
read this constructed literal (e.g., "
2000021918") into a TS value and convert that value to an IVL<TS> according to IVL_TS.promotionTS (e.g., "[2000021921;2000021922[") this is the "high interval." - phase is the convex hull of the low interval and the high
interval (e.g., "
[2000021918;2000021922["). - if the hull-operator was not present, phase is simply the low interval.
Interleave. A calendar pattern followed by a slash and an integer number n indicates that the given calendar pattern is to apply every nth time.
For example: "D19/2" is the 19th of every second month.
A calendar pattern expression is evaluated at the time the pattern is first encountered. At this time, the calendar digits missing from the left are completed using the earliest date matching the pattern (and following a preceding pattern in a combination of time sets).
For example: "D19/2" is the 19th of every second
month. If this expression is evaluated on March 14, 2000
phase is
completed to: "[20000319;20000320[/(2 mo)@DM" and thus
the two-months cycle begins with March 19, followed by May 19, etc. If
the expression were evaluated by March 20, the cycle would begin at
April 19, followed by June 19, etc.
If no calendar digits follow after the calendar period identifier, the pattern matches any date. The integer number following the slash indicates the length of the cycle. phase in these cases has only the width specified to be the duration of the anchoring calendar-cycle (e.g., in this example 1 day.)
For example: "CD/2" is every other day,
"H/8" is every 8th hour, for the duration of one hour.
Institution Specified Time. Both a PIVL literal and a calendar pattern may be followed by the three letters "IST" to indicate that within the larger calendar cycle (e.g., for "hour of the day" the larger calendar cycle is "day") the repeating events are to be appointed at institution specified times. This is used to specify such schedules as "three times a day" where the periods between two subsequent events may vary well between 4 hours (between breakfast and lunch) and 10 hours (over night.)
5.1.6
Periodic Intervals as Sets
The essential property of a set is that it contains elements. For non-aligned PIVLs, the contains-property is defined as follows. A TS t is contained in the PIVL if and only if there is an integer i for which t plus period times i is an element of phase.
|
For calendar-aligned PIVLs the contains property is defined using the calendar-cycle's sum(t, n) property that adds n such calendar cycles to the time t.
|
5.2
Event-Related Periodic Interval of Time (EIVL) specializes SET
Definition: Specifies a periodic interval of time where the recurrence is based on activities of daily living or other important events that are time-related but not fully determined by time.
For example, "one hour after breakfast" specifies the beginning of the interval at one hour after breakfast is finished. Breakfast is assumed to occur before lunch but is not determined to occur at any specific time.
|
5.2.1
Event : CS
Definition: A code for a common (periodical) activity of daily living based on which the event related periodic interval is specified.
Such events qualify for being adopted in the domain of this attribute for which all of the following is true:
- the event commonly occurs on a regular basis
- the event is being used for timing activities, and
- the event is not entirely determined by time
5.2.2
Offset : IVL<PQ>
Definition: An interval of elapsed time (duration, not absolute point in time) that marks the offsets for the beginning, width and end of the EIVL measured from the time each such event actually occurred.
For example: if the specification is "one hour before breakfast for 10 minutes" IVL.low of offset is 1 h and the IVL.width of offset is 10 min.
5.2.3
Literal Form
The literal form for an EIVL begins with the event code followed by an optional interval of the time-difference.
|
For example, one hour after meal would be
"PC+[1h;1h]". One hour before bedtime for 10 minutes:
"HS-[50min;1h]".
5.2.4
Resolving the Event-Relatedness
An EIVL is a set of time, that is, one can test whether a particular time or time interval is an element of the set. Whether an EIVL contains a given interval of time is decided using a relation event χ time referred to as EVENT(event, time). The property occurrenceAt(t) is the occurrence interval that would exist if the event occurred at time t.
|
Thus, an EIVL contains a TS t if there is an event time e with an occurrence interval v such that v contains t.
|
5.3
General Timing Specification (GTS) specializes SET<TS>
Definition: A <dt-TS>, specifying the timing of events and actions and the cyclical validity-patterns that may exist for certain kinds of information, such as phone numbers (evening, daytime), addresses (so called "snowbirds," residing closer to the equator during winter and farther from the equator during summer) and office hours.
GTS has the following aspects:
- GTS as a general SET<TS>. From this aspect GTS answers whether any given TS falls in the schedule described by the GTS value.
- GTS as the combination of multiple PIVLs. This aspect describes how both simple and complex repeat-patterns are specified with the GTS.
- GTS as a generator of a LIST<IVL<TS>>. From this aspect, GTS can generate all occurrence intervals of an event or action, or all validity periods for a fact.
- GTS as an expression-syntax defined for a calendar. This aspect is the GTS literal form.
In all cases GTS is defined as a SET<TS>. Using SET.union, SET.intersect and SET.difference, more complex SET<TS>s can be constructed from simpler ones. Ultimately the building blocks from which all GTS values are constructed are IVL, PIVL, and EIVL. The construction of the GTS value can be specified in the literal form. No special data type structure is defined that would generate a combination of simpler time-sets from a given GTS value. While any implementation would have to contain such a structured representation, it is not needed in order to exchange GTS values given the literal form.56
5.3.1
Convex Hull
A convex hull is the least interval that is a superset of all occurrence intervals. As noted in SET.hull, all totally ordered sets have a convex hull. Because GTS is a SET<TS>, which is totally ordered, all GTS values have a convex hull.
The convex hull of a GTS can less formally be called the "outer bound interval". Thus, the convex hull of a GTS describes the absolute beginning and end of the repeating schedule. For infinite repetitions (e.g., a PIVL) the convex hull has infinite bounds.
5.3.2
GTS as a Sequence of Occurrence Intervals
A GTS value is a generator of a sequence of time intervals during which an event or activity occurs, or during which a state is effective.
The nextTo-property maps to every point in time t the greatest continuous subset (an "occurrence interval") v of the GTS value S, where v is the interval closest to t that begins later than t or that contains t.
|
The nextAfter-property maps to every point in time t the greatest continuous subset (an "occurrence interval") v of theGTS value S, where v is the interval closest to t that begins later than t.
|
|
5.3.3
Interleaving Schedules and Periodic Hull
For two GTS values A and B we say that A interleaves B if their occurrence intervals interleave on the time line. This concept is visualized in Figure above.
For GTS values A and B to interleave the occurrence intervals of both groups can be arranged in pairs of corresponding occurrence intervals. It must further hold that for all corresponding occurrence intervals a ⊆ A and b ⊆ B, a starts before b starts (or at the same time) and b ends after a ends (or at the same time).
The interleaves-relation holds when two schedules have the same average frequency, and when the second schedule never "outpaces" the first schedule. That is, no occurrence interval in the second schedule may start before its corresponding occurrence interval in the first schedule.
With two interleaving GTS values, one can derive a periodic hull such that the occurrence intervals of the periodic hull is the convex hull of the corresponding occurrence intervals.
The periodic hull is important to construct two schedules by combining GTS expressions. For example, to construct the periodic interval from Memorial Day to Labor Day every year, one first needs to set up the schedules M for Memorial Day (the last Monday in May) and L for Labor Day (the first Monday in September) and then combine these two schedules using the periodic hull of M and L.
|
For two GTS values A and B where A interleaves B, a periodic hull is defined as the pair wise convex hull of the corresponding occurrence intervals of A and B.
|
The interleaves-relation is reflexive, asymmetric, and intransitive. The periodic hull operation is non-commutative and non-associative.57
5.3.4
Literal Form
The GTS literal allows specifying combinations of IVL<TS>, PIVL, and using the set operations union and intersection.58
Unions are speecified by a semicolon-separated list. Intersections are specified by a whitespace separated list. Intersection has higher priority than union. Set difference can be specified using a backslash; differences have an intermediate priority, i.e. weaker than intersection but stronger than union. Also parentheses can be used to overcome operator precedence when necessary.
|
The following table contains paradigmatic examples for complex GTS literals. For simpler examples refer to the literal forms of IVL, PIVL, and EIVL.
5.3.4.1
Symbolic Abbreviations for GTS expressions.
Table Table 47 defines symbolic abbreviations for GTS values that can be used in literals instead of their equivalent term. Abbreviations are defined for common periods of the day (AM, PM), for periods of the week (business day, weekend), and for holidays. The computation for the dates of some holidays, namely the Easter holiday, involve some sophistication that goes beyond what one would represent in a GTS literal. It is assumed that the dates of these holidays are drawn from some table or some generator module that is outside the scope of this specification.
These abbreviations are named GTS values and they can in turn be a factor of a GTS literal. For example, one can say "JHCHRXME H08..12" to indicate that the office hours on Christmas Eve is from 8 AM to 1PM only. And one can say "JHNUSMEM..JHNUSLBR" for the typical midwestern swimming pool season from Memorial Day to Labor Day.
NOTE: This table is not complete, nor does it include religious holidays other than Christian (of the Gregorian [Western] tradition) or national holidays countries other than those of the US. This is a limitation to be remedied by subsequent additions.
NOTE: Holidays are locale-specific. Exactly which religious holidays are subsumed under JH depends on the locale and other tradition. For global interoperability, using constructed GTS expressions is safer than named holidays. However, some holidays that depend on moon phases (e.g., Easter) or ad-hoc decree cannot be easily expressed in a GTS literal.
A
Informative Types
These types are currently marked as informative while known issues relating to their design are being resolved.
A.1
Parametric Probability Distribution (PPD) specializes T
Definition: A generic data type extension specifying uncertainty of quantitative data using a distribution function and its parameters. Aside from the specific parameters of the distribution, a mean (expected value) and standard deviation is always given to help maintain a minimum layer of interoperability if receiving applications cannot deal with a certain probability distribution.
For example, the most common college entrance exam in the United States is the SAT, which is comprised of two parts: verbal and math. Each part has a minimum score of 400 (no questions answered correctly) and a perfect score of 800. In 1998, according to the College Board, 1,172,779 college-bound seniors took the test. The mean score for the math portion of the test was 512, and the standard deviation 112. These parameter values (512, 112), tagged as the normal distribution parameters, paint a pretty good picture of test score distribution. In most cases, there is no need to specify all 1-million+ points of data when just 2 parameters will do!
Example for a parametric probability distribution
Note that the normal distribution is only one of several distributions defined for HL7.
Since a PPD specializes T, a simple T value is the mean (expected value or first moment) of the probability distribution. Applications that cannot deal with distributions will take the simple T value neglecting the uncertainty. That simple value of type T is also used to standardize the data for computing the distribution.
Probability distributions are defined over integer or real numbers and normalized to a certain reference point (typically zero) and reference unit (e.g., standardDeviation = 1). When other quantities defined in this specification are used as base types, the mean and the standardDeviation are used to scale the probability distribution. For example, if a PPD<PQ> for a length is given with mean 20 ft and a standardDeviation of 2 in, the normalized distribution function f(x) that maps a real number x to a probability density would be translated to f′(x′) that maps a length x′ to a probability density as f′(x′) = f((x′ - μ) / σ).
Where applicable, PPD conforms to the ISO Guide to the Expression of Uncertainty in Measurement (GUM) as reflected by NIST publication 1297 Guidelines for Evaluating and Expressing the Uncertainty of NIST Measurement Results. PPD does not describe how uncertainty is to be evaluated but only how it is expressed. The concept of "standard uncertainty" as set forth by the ISO GUM corresponds to standardDeviation.
A.1.1
Standard Deviation : QTY
Definition: The primary measure of variance/uncertainty of the value (the square root of the sum of the squares of the differences between all data points and the mean). standardDeviation is used to normalize the data for computing the distribution function. Applications that cannot deal with probability distributions can still get an idea about the confidence level by looking at standardDeviation.
standardDeviation is a specialisation of QTY (from T.diffType) that expresses differences between values of type T. If T is REAL or INT, T.diffType is also REAL or INT respectively. However if T is TS, T.diffType is a PQ in the dimension of time.
|
A.1.2
Probability Distribution Type : CE
Definition: A code specifying the type of probability distribution. Possible values are as shown in the attached table. The NULL value (unknown) for the type code indicates that the probability distribution type is unknown. In that case, standardDeviation has the meaning of an informal guess.
Table 49 lists the defined probability distributions. Many distribution types are defined in terms of special parameters (e.g., the parameters α and β for the γ-distribution, number of degrees of freedom for the t-distribution, etc.) For all distribution types, however, the mean and standard deviation are defined.
The three distribution-types unknown (NULL), uniform and normal must be supported by every system that claims to support PPD. All other distribution types are optional. When a system interpreting a PPD representation encounters a distribution type that it does not recognize, it maps this type to the unknown (NULL) distribution-type.
A.1.3
Literal Form
The general syntax of the literal form for PPD is as follows:
|
Examples: an example for a PPD<REAL> is "1.23(N0.005)" for a normal distributionType around 1.23 with a standardDeviation of 0.005. An example for a PPD<PQ> is "1.23 m (5 mm)" for an unknown distributionType around the length 1.23 meter with a standardDeviation of 5 millimeter. An example for a PPD<TS> is "2000041113(U4 h)" for a uniform distributionType around April 11, 2000 at 1pm with standardDeviation of 4 hours.
A.2
Probability Distribution over Real Numbers (PPD<REAL>) specializes PPD
type ParametricProbabilityDistribution<REAL> alias PPD<REAL>; |
The parametric probability distribution of real numbers is fully defined by the generic data type. However, there are some special considerations about literal representations and conversions of probability distributions over REALs, which are specified in this section.
A.2.1
Converting a real number (REAL) to an uncertain real number (PPD<REAL>)
When converting a REAL into a PPD<REAL>, PPD.standardDeviation is calculated from the REAL value's order of magnitude and REAL.precision (number of significant digits). Let x be a REAL with REAL.precision n. We can determine the order of magnitude e of x as e = log10 |x| where e is rounded to the next integer that is closer to zero (special case: if x is zero, e is zero.) The value of the least significant digit l is then l = 10e-n and the PPD.standardDeviation σ = l / 2.
A.2.2
Concise Literal Form
Besides the generic literal form of PPD<REAL>, a concise literal form is defined for PPD<REAL> over real numbers. This concise literal form is defined such that PPD.standardDeviation can be expressed in terms of the least significant digit in the mantissa. This literal is defined as an extension of the REAL literal:
|
Examples: "1.23e-3 (U5e-6)" is the uniform PPD.distributionType around 1.23 × 10-3 with 5 × 10-6 PPD.standardDeviation in generic literal form. "1.230(U5)e-3" is the same value in concise literal form.
A.3
Parametric Probability Distributions over Physical Quantities (PPD<PQ>) specializes PPD
PPD<PQ> is constructed from PPD. However, recognizing that the PQ.unit can be factored from the boundaries, we add additional semantics and a separate literal form. The additional view of a PPD<PQ> is a probability distribution over real numbers with one unit.
|
The unit applies to both mean and PPD.standardDeviation.
|
A.3.1
Concise Literal Form
A concise literal form for PPD<PQ> is defined based on the concise literal form of PPD<REAL> where REAL is the value. This literal is defined as an extension of the PQ literal.
|
Examples: "1.23e-3 m (N5e-6 m)" is the normal-distributed length of 1.23 × 10-3 m with 5 × 10-6 m PPD.standardDeviation in generic literal form. "1.230(N5)e-3 m" is the same value in concise literal form. "1.23e-3(N0.005e-3) m " is also valid; it is the concise literal form for PPD<PQ> combined with the generic literal form for PPD<REAL>.
A.4
Probability Distribution over Time Points (PPD<TS>) specializes PPD
type ParametricProbabilityDistribution<TS> alias PPD<TS>; |
PPD<TS> is fully defined by the generic data type. PPD.standardDeviation is of type TS.diffType, which is a duration (a PQ in the dimension of time.)
A.4.1
Converting TS to PPD<TS>
When converting a TS into a PPD<TS>, PPD.standardDeviation is calculated from the TS value's order of magnitude and precision (number of significant digits) such that two PPD.standardDeviations span the maximal time range of the digits not specified. For example, in 20000609 the unspecified digits are hour of the day and lower. All these digits together span a duration of 24 hours, and thus, PPD.standardDeviation ( is( = 12 h from 20000609000000.0000... up to 20000609999999.9999... (= 20000610)
This rule is different from that specified for REAL in that the range of uncertainty lies above the time value specified. This is to go with the common sense judgment that June 9th spans all day of June 9th with noon as the center, not midnight.
Endnotes
- [source] The HL7 Message Development Framework defines "update modes" for fields in a message. Note that because data values have neither identity nor state nor changing of state, these update modes do not apply for the properties of data values. Data values and their properties are never updated. A field of an object (e.g., a message) can be updated in which case the field's value is replaced by another value. But the value itself is never updated.
- [source] This is the reason why the ISO Abstract Syntax Notation 1 (ASN.1) is not an appropriate formalism for semantic data type specifications.
-
[source]
The data type definition language employed here is a conclusion of
experiments and experience with various alternatives. These
alternatives include data type definition tables and the use of the
Object Management Group's (OMG) Interface Definition Language
(IDL). The disadvantage of the data type definition tables was that
they gave the wrong impression of this specification being a
specification of abstract syntax rather than semantics. Conversely,
the disadvantage with IDL was that IDL gave the wrong impression of
this specification being an application programming interface (API)
definition.
The resulting data type definition language borrows significantly from IDL, the Object Constraint Language (OCL), JAVA, C++, and the parser generation tools LEX and YACC. It is inspired by features and style of these languages but amalgamating and augmenting these languages into precisely what is needed for this data type specification. The goal was a language that is minimal, and self-consistent. Also, as the main purpose of this language is to define data types it tries to get by without any built-in data types.
- [source] As can be seen, the type keyword is in place of IDL's and Java's interface and C++ amd Java's class keyword. The alias clause is unique to this specification as we do have the need for extremely short data type mnemonics in addition to more descriptive names. The specializes clause is preferred over C++ or IDL's colon clause as its meaning is more obvious.
- [source] Note that the IDL's notion of input and output arguments and IDL's, JAVA's and C++'s notion of return values and exceptions are all irrelevant concepts for this specification. The semantics of data types is not about procedure calls and parameter passing or normal and abnormal returns of control from a procedure body. Instead, each semantic property is conceptualized as a function that maps a value and optional arguments to another value. This mapping is not "computed" or "generated", it logically exists and we do not need to "call" such a function to actualize the mapping.
- [source] The restriction aspect of specialization deserves explanation. It is generally touted that inheritance should not retract properties that have been defined for the genus. This is still true for the restriction as properties are not actually retracted but constrained to a smaller value set. This may mean constraining properties to NULL, if NULL was an allowed value for that property in the parent type. In any case, logically, restriction is a specialization, with inheritance and substitutability.
- [source] Note the meaning of protected is a little different from the accessibility qualifiers (public, package, protected, private) as known from JAVA and C++. The protection used here is not about hiding the type information or barring properties defined by a protected type from access outside of this specification "package." It mainly is a strong recommendation not to declare attributes or other features of such protected types. Protected types should be used as "wrapped" in other types. The protected type is still directly accessible within the "wrap," no notion of "delegated properties" exists.
- [source] The invariant statement syntax and semantics is similar to the OCL "inv" clause. However, we did not use OCL in this specification for several reasons. (1) OCL syntax has a Smalltalk style that does not fit the C++/Java style of the data type definition language. (2) OCL has many primitive constructs and data types, while this specification avoids primitives as much as possible. (3) In part because of the richness in primitive constructs, OCL is fairly complex, more than is needed in this specification.
- [source] This construct is somewhat cyclical; there is a preexisting notion of Boolean values even though the Boolean is a type defined just like any other type. In addition, since this data type definition language is written in character strings, the notion of character strings pre-exists the definition of the character string type. These two types, character string and Boolean are therefore exceptional, but on the surface, they are defined just like any other data type. Since this data type specification language is not meant to be implemented, the cyclicality is not a real issue. Even if this language was implemented, one can use a "bootstrapping" technique as is common, e.g., for compilers that compile themselves.
- [source] Most of these syntactic features are in the spirit of the JAVA language, use of argument lists, curly braces to enclose blocks, semicolon to finish a statement, and the period to reference value properties. The double colon :: as used by C++ or IDL to distinguish between member-references and value-references are not used (as in Java). Unlike Java but like C++ and IDL, every statement is ended by a semicolon, including type declarations. Implicit type conversion is also retained from C++.
- [source] This means that if a one expects an ED value but actually has an ST value instead, one can turn the ST value into an ED.
- [source] The different grammars of literals are not meant to be combined into one overall HL7 value expression grammar. Although attempt have been made to resolve potential ambiguities between the literals of different types where they would be harmful, some of these ambiguities still remain. For example "1.2" can be a valid literal for both Object Identifier (OID) and a Real Number.
- [source] The BNF variant used here is similar to the YACC parser and LEX lexical analyzer generator languages but is simplified and made consistent to the syntax and declarative style of this data type definition language. The differences are that all symbols have exactly one attribute, their value strongly typed as one of the defined data types. Each symbol's type is declared in front of the symbol's definition (e.g.: INT digit : "0" | "1" | ... | "9";). The start symbol has no name but just a type (e.g., INT : digit | INT digit;). A data type name can occur as a symbol name meaning a literal of that data type.
- [source] Note that the equal property (defined for all data types, see equal) is a relation, a test for equality, not an assignment statement. One can not assign a value to another value. Unlike YACC and LEX analyzers, this data type definition language is purely declarative it has no concept of assignment. For this reason, the grammar rules define both parsing and building literal expressions.
- [source] Generic type extensions are sometimes called "mixins", since their effect is to mix certain properties into the preexisting data type.
- [source] The cryptographically strong checksum algorithm Secure Hash Algorithm-1 (SHA-1) is currently the industry standard. It has superseded the MD5 algorithm only a couple of years ago, when certain flaws in the security of MD5 were discovered. Currently the SHA-1 hash algorithm is the default choice for the integrity check algorithm. Note that SHA-256 is also entering widespread usage.
- [source] RFC 3066 [http://www.ietf.org/rfc/rfc3066.txt] is the HL7-approved coding system for all reference to human languages, in data types and elsewhere.
- [source] For this reason, a system or site that does not deal with multilingual text or names in the real world can safely ignore the language property.
- [source] The cryptographically strong checksum algorithm Secure Hash Algorithm-1 (SHA-1) is currently the industry standard. It has superseded the MD5 algorithm only a couple of years ago, when certain flaws in the security of MD5 were discovered. Currently the SHA-1 hash algorithm is the default choice for the integrity check algorithm. Note that SHA-256 is also entering widespread usage.
-
[source]
ISO/IEC 10646-1: 1993 defines a character as "A member of a set of
elements used for the organization, control, or representation of
data." ISO/IEC TR 15285 - An operational model for characters and
glyphs. Discusses the problems involved in defining
characters. Notably, characters are abstract entities of information,
independent of type font or language. The ISO 10646 (UNICODE
[http://www.unicode.org]) - or in Japan, JIS X0221 - is a globally
applicable character set that uniquely identifies all characters of
any language in the world.
In this specification, ISO 10646 serves as a semantic model for character strings. The important point is that for semantic purposes, there is no notion of separate character sets and switching between character sets. Character set and character encoding are ITS layer considerations. The formal definition gives indication to this effect because each character is by itself an ST value that has a charset property. Thus, the binary encoding of each character is always understood in the context of a certain character set. This does not mean that the ITS should represent a character string as a sequence of full blown ED values. What it means is that on the application layer the notion of character encoding is irrelevant when we deal with character strings.
- [source] RFC 3066 [http://www.ietf.org/rfc/rfc3066.txt] is the HL7-approved coding system for all reference to human languages, in data types and elsewhere.
- [source] For this reason, a system or site that does not deal with multilingual text or names in the real world can safely ignore the language property.
- [source] An ST literal is a conversion from a character string to another data type. Obviously, ST literals for character strings is a cyclical if not redundant feature. This literal form, therefore, mainly specifies how character strings are parsed in the data type specification language.
- [source] The advantage of the CD data type is its expressiveness, however, if all of its features, such as coding exceptions, text, translations and qualifiers are used at all times, implementation and use become very difficult and unsafe. Therefore, CD is most often used in a restricted form with reduced features.
- [source] codeSystemVersion does not count in the equality test since by definition a code symbol must have the same meaning throughout all versions of a code system. Between versions, codes may be retired but not withdrawn or reused.
- [source] Translations are not included in the equality test of concept descriptors for safety reasons. An alternative would have been to consider two CD values equal if any of their translations are equal. However, some translations may be equal because the coding system of that translation is very coarse-grained. More sophisticated comparisons between concept descriptors are application considerations that are not covered by this specification.
- [source] NULL-values are exceptional values, not proper concepts. It would be unsafe to equate two values merely on the basis that both are exceptional (e.g., not codable or unknown.) Likewise there is no guarantee that original text represents a meaningful or unique description of the concept so that equality of that original text does not constitute concept equality. The reverse is also true: since there is more than one possible original text for a concept, the fact that original text differs does not constitute a difference of the concepts.
- [source] This ruling at design-time is necessary to prevent HL7 interfaces from being burdened by code literal style conversions at runtime. This is notwithstanding the fact that some applications may require mapping from one form into another if that application has settled with the representation option that was not chosen by HL7.
- [source] This is one reason why qualifier is to be used sparingly for post-coordination and with caution. An additional problem of post-coordinated coding is that a general rule for equality may not exist at all.
- [source] This is not withstanding the fact that an external referenced domain, such as the IETF MIME media type may include an extension mechanism. These extended MIME type codes would not be considered "extensions" in the sense of violating the CNE provision. The CNE provision is only violated if an attempt is made in using a different code system (by means of CD.codeSystem), which is not possible with CS.
- [source] The value/namespace view on ISO object identifiers has important semantic relevance. It represents the notion of identifier value versus identifier assigning authority (= namespace), which is common in healthcare information systems in general, and HL7 v2.x in particular.
- [source] DICOM objects are identified by UID only. For the purpose of DICOM/HL7 integration, it would be awkward if HL7 required the extension to be mandatory and to consider the UID only as an assigning authority. Since UID values are simpler and do not contain the risks of containing meaningless decoration, we do encourage systems to use simple UID identifiers as external references to their objects.
-
[source]
This ruling at design-time is necessary to prevent HL7 interfaces from
being burdened by identifier literal style conversions at
runtime. This is notwithstanding the fact that some applications may
require mapping from one form into another if that application has
settled with the representation option that was not chosen by HL7.
From practical experience it is recommended that II.extensions as an alphanumeric identifier not contain leading zero digits (if any zeroes at all), for these are often erroneously stripped. "000123" and "123" would be different extension values, but this is prone to be misunderstood, leading to false non-matches and duplicate record entries. However applications should maintain any leading zero digits encountered in II extensions. Leading zero digits are prohibited in OID's, but may occur in UUID's, where they must be maintained.
There is no separate check digit property. Check digits are used for human purpose and work best if kept completely transparent. II.extensions MAY contain check digits anywhere, and the particular check digit scheme (if any) would be implied by the II.root. However, a separate check digit property is intentionally not recognized by this specification.
- [source] The data type of the scheme is still CS and for HL7 purposes, the scheme is a CNE domain. This appears to be at odds with the fact that there is no one official list of URL schemes, and so many URL schemes in use may be defined locally. However, we cannot allow extension of the URL scheme using the HL7 mechanism of local alternative code systems, which is why technically the scheme is a CS data type.
- [source] Remember that semantic properties are bare of all control flow semantics. The formatted could be implemented as a "procedure" that would "return" the formatted address, but it would not usually be a variable to which one could assign a formatted address. However, HL7 does not define applications but only the semantics of exchanged data values. Hence, the semantic model abstracts from concepts like "procedure", "return", and "assignment" but speaks only of property and value.
- [source] Remember that semantic properties are bare of all control flow semantics. The formatted could be implemented as a "procedure" that would "return" the formatted address, but it would not usually be a variable to which one could assign a formatted address. However, HL7 does not define applications but only the semantics of exchanged data values. Hence, the semantic model abstracts from concepts like "procedure", "return", and "assignment" but speaks only of property and value.
- [source] These rules for formatting addresses are part of the semantics of addresses because addresses are primarily defined as text displayed or printed and consumed by humans. Other uses (e.g., epidemiology) are secondary — although not forbidden, the AD data type might not serve these other use cases very well, and HL7 defines better ways to handle these use cases. Note that these formatting rules are not ITS issues, since this formatting applies to presentations for humans whereas ITS specifications are presentations for computer interchange.
- [source] The XML encoding shown here is according to the XML ITS only in order to avoid introducing another instance notation. This does not imply that the function would only work in XML, nor even that XML is the preferred representation.
- [source] This example shows the strength of the mark-up approach to addresses. A typical German system that stores house number and street name in separate fields would print the address with street name first followed by the house number. For U.S. addresses, this would be wrong as the house number in the U.S. is written before the street name. The marked-up address allows keeping the natural order of address parts and still understanding their role.
- [source] Remember that semantic properties are bare of all control flow semantics. The formatted could be implemented as a "procedure" that would "return" the formatted name, but it would not usually be a variable to which one could assign a formatted name. However, HL7 does not define applications but only the semantics of exchanged data values. Hence, the semantic model abstracts from concepts like "procedure", "return", and "assignment" but speaks only of property and value.
- [source] Remember that semantic properties are bare of all control flow semantics. The formatted could be implemented as a "procedure" that would "return" the formatted name, but it would not usually be a variable to which one could assign a formatted name. However, HL7 does not define applications but only the semantics of exchanged data values. Hence, the semantic model abstracts from concepts like "procedure", "return", and "assignment" but speaks only of property and value.
- [source] These rules for formatting names are part of the semantics of names because the name parts have been designed with the important use case of displaying and rendering on labels. Note that these formatting rules are not ITS issues, since this formatting applies to presentations for humans whereas ITS specifications are presentations for computer interchange.
- [source] The quantity data type abstraction corresponds to the notion of difference scales in contrast to ordinal scales and ratio scales (Guttman and Stevens). A data type with only the order requirement but not the difference requirement would be an ordinal. Ordinals are not currently defined with a special data type. Instead, ordinals are usually coded values, where the underlying code system specifies ordinal semantics. This ordinal semantics, however, is not reflected in the HL7 data type semantics at this time.
- [source] H. Grassman. Lehrbuch der Arithmetik. 1861. We prefer Grassman's original axioms to the Peano axioms, because Grassman's axioms work for all integers, not just for natural numbers. Also, "it is rather well-known, through Peano's own acknowledgment, that Peano borrowed his axioms from Dedekind and made extensive use of Grassmann's work in his development of the axioms." (Hao Wang. The Axiomatization of Arithmetic. J. Symb. Logic; 1957:22(2); p. 145.)
- [source] The term "Real" for a fractional number data type originates and is well established in the Algol, Pascal tradition of programming languages.
- [source] Imagine a special clock that measures those cycles, where the pointers are not all stacked on a common axis but each pointer is attached to the end of the pointer measuring the next larger cycle.
- [source] At present, the CalendarCycle properties sum and value are not formally defined. The computation of calendar digits involves some complex computation which to specify here would be hard to understand and evaluate for correctness. Unfortunately, no standard exists that would formally define the relationship between calendar expressions and elapsed time since an epoch. ASN.1, the XML Schema Data Type specification and SQL92 all refer to ISO 8601, however, ISO 8601 does only specify the syntax of Gregorian calendar expressions, but not their semantics. In this standard, we define the syntax and semantics formally, however, we presume the semantics of the sum-, and value-properties to be defined elsewhere.
- [source] At this time, no other calendars than the Gregorian calendar are defined. However, the notion of a calendar as an arbitrary convention to specify absolute time is important to properly define the semantics of time and time-related data types. Furthermore, other calendars might be supported when needed to facilitate HL7's use in other cultures.
- [source] In some programming languages, "collection types" are understood as containers of individually enumerated data items, and thus, an interval (low - high) would not be considered a collection. Such narrow interpretation of "collection" however is heavily representation/implementation dependent. From a data type semantics viewpoint, it doesn't matter whether an element of a collection "is actually contained in the collection" or not. There is no need for all elements in a collection to be individually enumerated.
- [source] Note the difference to the GTS. The GTS is a generator for a SET<TS> not for a LIST<TS>. A sequence of discrete values from a continuous domain makes not much sense other than in sampling applications. The SET<TS>, however, can be thought of as a sequence of IVL<TS>, which still is different from a LIST<TS>.
-
[source]
The presence of so many options deserves explanation. In principle,
the interval form together with the width-only form would be
sufficient. However, the interval form is felt alien to many in the
field of medical informatics. One important purpose of the literal
forms is to eradicate non-compliance through making compliance easy,
without compromising on the soundness of the concepts.
Furthermore, the different literal forms all have strength and weaknesses. The interval and center-width forms' strength is that they are most exact, showing closed and open boundaries. The interval form's weakness, however, is that infinite boundaries require special symbols for infinities, not necessary in the "comparator" form. The center-width form cannot specify intervals with an infinite boundary at all. The "comparator" form, however, can only represent single-bounded intervals (i.e., where the other boundary is infinite or unknown.) The dash form, while being the weakest of all, is the most intuitive form for double bounded intervals.
- [source] This statement seems to directly contradict the ruling about the promotion of TS to IVL<TS>. However, there is no contradiction. The precision of a boundary does not have any relevance, but the precision of a simple timestamp (not as an interval boundary) is relevant, when that timestamp is promoted to an interval.
- [source] The hull form may appear superfluous for the simple interval all by itself. However, the hull form will become important for the periodic interval notation as it shortens the notation and (perhaps arguably) makes the notation of more complex timing structures more intuitive.
- [source] This specification imposes a self-restraint upon itself to allow existing systems a graceful transition. However, the formal specification keeps the generic type extensions as substitutable for their base types. This self-restraint may be omitted in the future. New implementations are advised to accommodate some generalizable support for these generic data type extensions.
- [source] Note that data types are specifications of abstract properties of values. This specification does not mandate how these values are represented in an ITS or implemented in an application. Specifically, it does not mandate how the represented components are named or positioned. In addition, the semantic generalization hierarchy may be different from a class hierarchy chosen for implementation (if the implementation technology has inheritance.) Keep the distinction between a type (interface) and an implementation (concrete data structure, class) in mind. The ITS must contain a mapping of ITS defined features of any data type to the semantic properties defined here.
- [source] GTS is an example of a data type that is only defined algebraically without giving any definition of a data structure that might implement the behavior of such a data type. The algebraic definition looks extremely simple, so that one might assume it is incomplete. Since at this point we are relying entirely on the literal form to represent GTS values, all the definition of data structur
- [source] The interleaves property may appear overly constrained. However, these constraints are reasonable for the use case for which the interleaves and periodic hull properties are defined. To safely and predictably combine two schedules one would want to know which of the operands sets the start points and which sets the endpoints of the periodic hull's occurrence intervals.
- [source] This literal specification again looks surprisingly simple, so one might assume it is incomplete. However, the GTS literal is based on the TS, IVL, PIVL, and EIVL literals and also implies the literals for the extensions of TS, notably the PPD<TS>. The GTS literal specification itself only needs to tie the other literal forms together, which is indeed a fairly simple task by itself.